CES生产函数

---

设y为产量，l为劳动投入量和k为资本投入量，如果生产技术表现为：

y=A[αk^－β+(1－α)l^－β]^－1／β

其中0＜α＜1，－1＜β＜∞，A＞0，则称它为CES生产函数。

它有如下性质

(1)对λ＞0有：

A[α(λk)^－β+(1－α)(λ1)^－β]^1／β

=λA[αk^－β+(1－α)1^－β]^－1／β

故它是一阶齐次的生产函数。

(2)由于

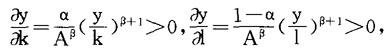
故它的要素边际产品为正。

(3)要素的替代弹性：

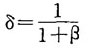
即要素的替代弹性δ为常数，这就是不变替代弹性(constant elasticity of substitution，简写为CES)生产函数名称的来源。

(4)当β→－1时，y趋于线性函数。

(5)当β→0时，y趋于柯布－道格拉斯生产函数。

(6)当β→∞时，y趋于里昂惕夫生产函数。