化二次型为标准形、规范形

---

二次型的标准形、规范形 二次型f(x₁，x₂，…，x_n)=x^TAx经可逆线性变换x=Cy，化成(消去混合项)，称为二次型的标准形．

di=1，－1，0的标准形，称为二次型的规范形．

化二次型为标准形，即对实对称矩阵A，求可逆矩阵C，使得C^TAC=A，其中是对角阵．

任何一个n元二次型都可以通过可逆线性变换x=Cy化成标准形，即．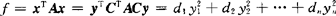

即对任一个实对称矩阵A，都存在可逆矩阵C，使得

C^TAC=diag(d₁，d₂，…，d_n)．

注d₁，d₂，…，d_n一般不是A的特征值．

化二次型为标准形、规范形的方法

(1)配方法(要点)

若f中有平方项，则将该平方项及与其有关的混合项一起配成完全平方，使配完完全平方后，减少一个变量．总的完全平方的项数少于等于变量的个数．若f中没有平方项，则令

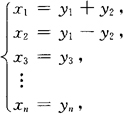
使f经变换后出现平方项，以后再配完全平方．配完完全平方后，令每个平方项的一次式分别为z₁，z₂，…，z_n(若完全平方项次数少于变量个数时，应补足成n个)，则必可将二次型化成标准形，所做的可逆线性变换矩阵，可由所做的变换得到．

(2)初等变换法(要点)

将二次型的对应矩阵A，通过一系列的相同类型的初等行、列变换可以化成合同标准形(对角矩阵)，所谓相同类型的初等行、列变换是指：

A的第i行乘k倍(k≠0)，则第i列也乘k倍；

A的第i，j行对换，则第i，j列也对换；

A的第i行的c倍加到第j行，则第i列的c倍也加到j列．

若将A，E写成(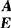)，对(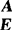)实施列变换，并对A做相同类型的行变换，将A化成对角阵时，E就变成了可逆线性变换矩阵C，即

则 f(x₁，x₂，…，x_n)=x^TAx

正交变换 对任一个n元实二次型

存在正交变换x=Qy(其中Q是n阶正交矩阵)，使得

其中λ_i(i=1，2，…，n)是A的特征值，Q的列向量是A的对应于λ_i的标准正交特征向量．

二次型通过正交变换化标准形的步骤：

(1)写出二次型f的对应矩阵A；

(2)求A的特征值λ_i；

(3)求A的特征向量ξ_i；

(4)将重根的特征向量正交化；

(5)将所有特征向量单位化，记为；

(6)取，并令x=Qy；

(7)得．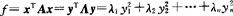

注 正交变换法一般只能化二次型为标准形，不能化成规范形．

惯性定理 对于一个n元二次型x^TAx，不论做怎样的可逆线性变换化成标准形(或规范形)，其中正平方项项数p，负平方项项数q都是惟一确定的，或对任一个n阶实对称矩阵A，无论取怎样的可逆矩阵C，使

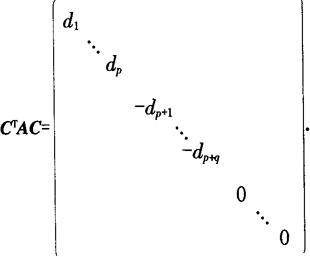
其中d_i＞0(i=1，2，…，p+q)，p+q=r≤n，则p，q是由A惟一确定的．

正惯性指数，负惯性指数，负号差

二次型化标准形，标准形中正项项数称为正惯性指数，负项项数称负惯性指数，正、负惯性指数的差称为符号差．

实对称矩阵合同于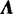若A是n阶实对称矩阵，有正、负惯性指数分别为p．q，则，

其中1有p个，－1有q个，0有n－(p+q)个，r=p+q是A的秩r(A)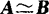．的充要条件 两个实对称矩阵A，B合同(即其对应的二次型f=x^TAx，g=y^TBy合同)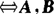有相同的正惯性指数和相同的负惯性指数．

按合同关系分类 全体n元二次型(全体n阶实对称矩阵)按合同关系，即按合同规范形(不考虑+1，－1，0的排列次序)分类，共有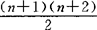类．

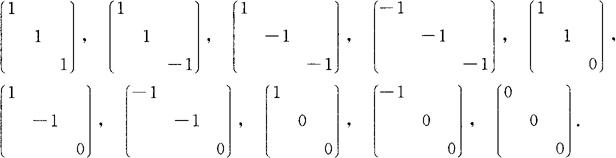
全体三元二次型(全体三阶实对称矩阵)按合同关系分类，共有类．它们的合同规范形分别是