量词模态逻辑的代数语义学

---

模态逻辑是研究“必然”与“可能”等模态概念的逻辑学说。

模态逻辑有著悠久的历史。亚里士多德在创建形式逻辑时就用了比实然逻辑多两倍的篇幅来讨论模态逻辑，但后来被忽视了。20世纪初刘易斯(C．I．Lewis)为了摆脱实质蕴涵悖论而引进模态概念，从而定义了严格蕴涵以代替实质蕴涵。并于1932年与兰福德(C．M．Langford)合著《符号逻辑》一书，提出了S1－，S5等5个著名模态命题逻辑系统，才使模态逻辑得以复兴。

60年代以前，模态逻辑的研究主要限于命题模态逻辑；极少论及量词模态逻辑的工作，而且成果也甚少。

40年代麦克铿赛(J．C．C．McKinsey)和塔尔斯基(A．Tarski)对刘易斯的系统S2与S4引进了代数语义。

假设S为一个非古典命题逻辑系统。以由叠合S中之等价公式而得的S的Lindenbaum-Tarski代数(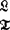)〔S，｛p_i｜i∈I｝〕为自由代数的那一类泛代数(universal algebras)称为S代数。

作为格来说为完备的5代数称为S^*代数。

显然，如果系统S的任一公式φ当看作任一S代数A上的多项式Φ_φ时恒取A的幺元(即最大元)V为值，则φ必定是S的定理，即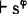，这是因为作为S代数中的一员的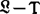代数(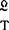)〔S，｛p_i｜i∈I｝〕是系统S的特征代数模型。因而S的代数语义完全性定理便十分容易得到了。早在40年代就已知道S4代数就是闭包代数(即拓朴布尔代数)；而高恒珊1963年又指出S5(即S_ε)代数就是哈尔姆斯(P．R．Halmos)1955年提出的一目布尔代数monadic Boolean algebras)；费斯(R．Feys)1938年提出的系统T的相应代数则于1960年被莱蒙(E．J．Lemmon)称为外延代数(extension algebra)。

1959年克瑞普克(Saul A．Kripke)发表了题为“模态逻辑中的一个完全性定理”的论文。此文的重大意义在于首次对一阶模态系统提出可能世界(possible worlds)语义(亦称关系语义)并对基于刘易斯系统S5之上的量词理论S5*证明了相对于此种语义的完全性定理。

早在1953年拉西阿娃(H．Rascowa)等便用代数方法研究了S4(即S_λ)的量词理论S4^*的代数语义完全性问题。同时被研究的非古典逻辑尚有正演算S_π、海丁(A．Heyting)直觉主义演算S_x和约翰逊(J．Johanson)的极小演算S_μ等，相应代数分别为相对假补格、海丁代数(亦称假布尔代数)以及约翰逊代数。

拉西阿娃等对基于一般命题逻辑S之上的谓词逻辑S^*所提出的代数语义可溯源于1948年莫斯托夫斯基(A．Mostowski)关于某语句σ在海丁谓词演算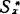中不可证的论证方法。其方法为：选取一非空集J，一个完备海丁代数A，让个体变元在J中变动；对任何语句φ把φ中出现的每个k(≥1)目谓词字母P^(k)解释为定义在J的k重卡氏积J^k上而在A中取值的映射(函数)(p^(k)：J^k→A；把命题联结词解释为A上的相应格运算，存在(或全称)量词解释为A中相应元素集的最小上界(或最大下界)。

在这种解释下莫氏证明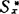中的任一可证公式均恒取A中幺元V为值，而σ却不然，从而得出σ在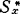中不可证。拉西阿娃等把这一代数处理方法用于上述诸非古典逻辑，并证明对与这些系统相似的任一系统S，如果S具有某种性质(E)则对每个语句φ，若对任何非空个体集J，任何完备S代数，即S^*代数A和任一解释μ，使得对于φ中每个谓词字母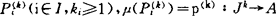，均有(J，A)Φ_φ(｛p_i^(ki)｜i∈I｝)=VA中的幺元，则必有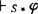，即φ在S^*中可证，或曰对于量词系统S^*而言哥德尔(K．Gödel)型完全性定理成立。

1953年拉西阿娃等证明了上述诸系统(包括S_λ即S4)皆有性质(E)，从而对它们得到了哥德尔型完全性定理。1963年高恒珊运用哈尔姆斯关于一目布尔代数的表示定理证明了S5(即S_e)具有比(E)稍弱的性质(σE)，从而对量词理论S5^*证明了哥德尔型完全性定理。1964年他又进一步证明上面的代数A可取为域为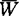的Z值全函项单纯一目布尔代数2^w，而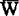可取为任一可数无穷集，比如ω₁(=ω₀)即可。因2^w为单纯S5^*代数，所以我们称量词系统S5^*为单纯完全的。

继1959年的工作之后，克瑞普克又于1963年对正规模态命题演算S=T，S4，B，S5提出了语义分析。考虑如下公理模式和推理规则：A0．全部重言式，，，，，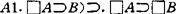

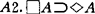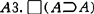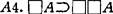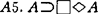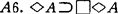，；R1，Modus Ponens，R2．A／□A。定义T=｛A0，A1，A3；R1，R2｝，S4=TU｛A4｝，B=TU｛A5｝，S5=TU｛A6｝=TU｛A4，A6｝，克氏称一模态系统为正规模态系统，如果它包含T的全部定理且在R1，R2下封闭(后来正规性的条件又放宽为：包含公理A0，A1且在R1、R2下封闭)。显然上述四系统均为正规模态系统。

此类系统的克瑞普克语义(即关系语义)基于模型结构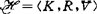，此处K为非空集，其元素称为可能世界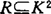，为K上的二元关系，V为在任一可能世界w_i∈K上对命题字母P_i的真值指派，V(w_i，P_i)=0或1(0为假，1为真)。模型结构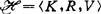叫做T(或54，B，S5)模型结构，如果其中关系R为自反的(或自反且传递的、自反且对称的，等价关系)。

指派V可扩充至任何模态公式如下：V(w_i，～A)=1 iffV(w_i，A)=0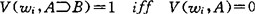；或(w_i，B)=1；V(w_i，□A)=1iff对任何w_j∈K，若w_iR w_j成立则V(w_j，A)=1；V(w_i，◇A)=1 iff存在w_j∈K，适合w_iRw_j，且V(w_j，A)=1，可以证明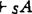，(此处S表示T^′S4，B，S5之一)，当且仅当对任何S模型结构μ=〈K，R，V〉均有V(w，A)=1对任何w∈K。克瑞普克对这几个语义完全性定理的证明采用语义局面(Semantic tableaux)方法，难而且长。

1966年莱蒙(E．J．Lemmon)发表题为“模态逻辑的代数语义学Ⅰ／Ⅱ”两篇文章，文章一开始便指出该系列文章的宗旨是把模态逻辑中已有的最深刻的两种语义，即代数语义和克瑞普克的关系语义加以综述，虽然也有新结果，但“旨趣宁可说是在于揭示了熟知结果间的联系，提供进一步研究的体制。一般来说，我们要证明克瑞普克型语义完全性结果可以由代数结果借助于一个中心定理(定理21)推出。

”在此两文中，他一共讨论了18个模态系统，其中最强的4个就是T，S4，B和S5。所有这些系统的克氏语义完全性的证明在他的文章中因使用了定理21而大大简化了。

他并且“希望用第3篇文章来讨论添加量词于所有这些系统”。遗憾的是由于这位知名模态逻辑专家英年早逝，他的希望并未实现。

为了实现莱蒙的愿望，高恒珊于1987年首先在系统S5^*的代数语义与克氏的关系语义间确立了相互可转化性。设Ω_ρ=〈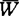，J，V〉为S5^*的任一模型结构，此处W为可能世界组成的任意非空集；J为由个体组成的非空集；V为Ω_p上的指派，即对于任何谓词字母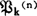，有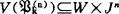。另一方面，引进一个固定的S5^*代数2^w，它就是前面提到的单纯一目布尔代数。考虑S5^*的代数模型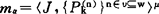此处μ为如下指派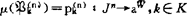：。则有如下转化：

(Ⅰ)设Ω_ρ=〈W，J，V〉为S5^*的一个模型结构。今定义一相应代数模型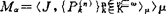此处对任一谓词字母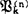有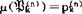，使得对任何个体a₁，…，a_n∈J有

。

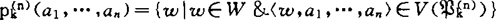(Ⅱ)设已有代数模型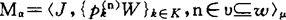则可得一相应模型结构Ω_ρ=〈W，J，V〉如下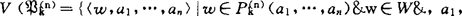：…，a_n∈J｝

设σ为一语句，则以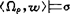表示σ在关系模型〈Ω_ρ，w〉上为真亦即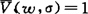，以σ｜_mα表示σ在代数模型m_α上的值即

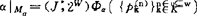则由(Ⅰ)或(Ⅱ)均能推出如下事实：

定理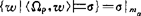

由此得：由克瑞普克1959年关于S5^*的完全性定理可推出高恒珊1964年关于S5^*(即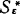)的单纯完全性定理，反之亦然，即该两个完全性定理可以互推。

1988年吕健安对高恒珊的上述工作作了推广。设以BF简记如下的所谓巴尔坎公式(Barcan Formula)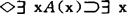：◇A(x)。他考虑了带有公式BF的正规量词模态系统的哥德尔型代数完全性定理的成立与否的问题。

为了证明该定理，若用拉西阿娃等人1953年的方法则要验证性质(E)(或较弱的条件(σE))而这一般来说是十分困难的。但是对于由象系统K=｛A0，A1；R1，R2｝，T(D)=｛A0，A1，A2；R1，R2｝，K4=｛A0，A1，A4；R1，R2｝以及T，S4，B等正规模态系统经添加巴尔坎公式BF而得到的量词模态系统K+BF，(T(D)+BF，K4+BF，T+BF，S4+BF以及B^*(注意BF在B^*中可证))其相应的克瑞普克关系语义完全性定理的证明如休斯(G．E．Hughes)等著《模态逻辑引论》一书第9章所述是有一般方法可循的。此时若采用上述由克氏语义向代数语义的转化(Ⅰ)便可得到和上述定理相当的结论，从而得到相应系统的代数语义完全性定理。

事实上，若以S^*表示上述6个带(或含)BF的正规量词模态系统之任一个，以Ω_ρ=〈W，R，J，V〉表示S^*的任何克氏模型结构，其中R为W上的二元关系，使得在S^*=K+BF情形R为任何关系，而S^*为T(D)+BF(或K4+BF，T+BF，S4+BF，B^*)情形，R限于系列的(serial，即对任何w∈W均存在一w′∈W使得wRw′)(或传递的，自反的，自反且传递的，自反且对称的)关系。

其实S5^*(亦含BF)亦属此类情形，只不过此时R=W×W故把R略去了。考虑带算子P的布尔代数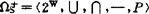∪，∩，－，P〉，这里∪，∩，－分别表示W的全部子集的类2^W上的求并、交、补的运算而对任何A∈2^w(即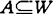)有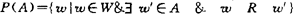，定义N(A)=－P(A)则可证明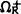为S^*代数。

定义S^*的代数模型m_α=〈J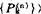，，此处赋值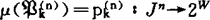，使得对任何a₁，…，a_n∈J有

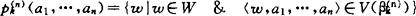。须注意者为，在(J，2^W)Φ泛函的定义中当φ=◇Ψ时有：

。

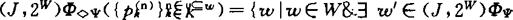
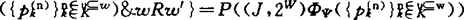则同上面一样可证明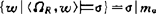：因而如果语句σ对任何代数模型皆有效则应有σ｜m_α=W，从而可见σ为Ω_p有效的。因Ω_p为S^*的任意克氏模型结构，可知σ为克氏语义永真的，从而由S^*的相应克氏语义完全性定理知应有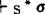，从而S^*为代数语义完全的。

剩下来的问题是关于非正规量词模态系统(同样带公式BF)的情形。这项工作尚未开始，估计无太大困难。

这样我们看到莱蒙的上述未竟之业已接近完成。最后关于不带BF的量词模态系统，则因其克氏语义中之个体域J随可能世界而变，从而其代数语义学亦应有所变动。结果如何尚待进一步的研究。

。【参考文献】：

1 Mckinsey J C C. J of Symbolic hgic,1941,6:117～134

2 Mckinsey J C C, etal. Ibid,1948,13:1 ～15

3 Mostowski A. Ibid,204～207

4 Rasiowa H , et al. Fund Math,1953,40:62～95

5 Halmos P R. Compositlo Math, 1955,12:217～249

6 Kripke S A . der Math, 1963,9:67 ～ 96

7 高恒珊．数学学报，1963，13∶68～77

8 高恒珊．Ibid，1964，14∶546～548

9 高恒珊．Ibid，1987，30∶938～846

10 吕健安等．Ibid，1988，31∶692～698

(中国科技大学研究生院高恒珊教授撰)

上一篇：中介公理集合论
下一篇：现代科技综述大辞典上目录

"量大福也大，机深祸亦深量大福也大，机深祸亦深

---

旧谓气度大的人福气也大；搅动心机算计他人者必遭祸殃。

元末明初·施耐庵、罗贯中《水浒全传》第十九回：“可怜王伦做了多年寨主，今日死在林冲之手，正应古人言：‘量大福也大，机深祸亦深。’”明·凌濛初《二刻拍案惊奇》卷三十六：“量大福亦大，机深祸亦深。法轮用了心机，藏了别人的宝镜，自然发了家。

天理不容，自然生出事端来。

”