采样系统的稳定性

---

(1)系统稳定的必要充分条件

由于s平面虚轴在z平面的映象为单位圆，s平面左半部映射到z平面的单位圆内部，s平面右半部在z平面的映象为单位圆外部，如图5．7－10(a)、(b)所示。因此，对于采样控制系统，其稳定的必要充分条件是系统脉冲传递函数的极点应全部位于z平面的单位圆内。z平面上单位圆周为稳定域的边界，如系统有极点在z平面的单位圆外或单位圆上，则系统不稳定。

(2)稳定性的代数判据

若采样系统的特征方程为

a_nzⁿ+a_n1z^”－1+…+a₁z+a₀=0(5．7－20)

为判别其根是否在单位圆内，须取如下的所谓双线性变换，即令

［解］系统连续部分的开环传递函数为

查表5．7－1可得系统开环脉冲传递函数为

式中 T——采样周期；

T₁——图5．7－11所示系统连续部分惯性环节的时间常数。

查表5．7－3第一栏，令H(s)=1，得闭环系统脉冲传递函数为

其特征方程为

将上式进行z-w变换并整理后得

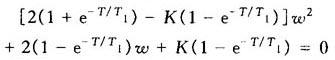
由劳斯判据可知，对于二阶系统，只要特征方程的各项系数均大于零，系统就是稳定的。由于(1－e^－T／T₁)＞0，所以为使系统稳定，必须满足

［2(1+_e^－T／T₁)－K(1－e^－T／T₁)］＞0

解上述不等式，并考虑K＞0，得该系统稳定时K的变化范围为

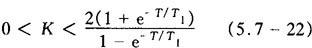
对上例的分析可有如下结论：对没有采样器的二阶连续系统，只要K大于零，系统总是稳定的，但当系统增加采样器变成采样系统后，开环增益被限制在式(5．7－22)要求的范围之内系统才稳定。一般说来，引入采样器会降低系统的稳定性，且采样周期越大，系统稳定性越差。不过，实践证明，对于带有很大时间延迟(大滞后)对象的系统则例外。