为了证明的需要,在原来图形上添画的线叫做辅助线.
注意 1.当问题条件不够时,添加辅助线,构造新图形,形成新关系,找到已知与未知的桥梁,把问题转化成自己已经会解的情况,这是解决问题常用的方法之一.
2.辅助线的添法没有统一的规律,要根据实际需要而定.
3.对于一个证明来讲,其辅助线的做法未必惟一.
4.辅助线通常画成虚线.
例 如图所示,在△ABC中,∠A=2∠B,CD是∠ACB的平分线.
求证:BC=AC+AD.
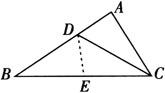
证明 在BC上截取CE=AC,连接DE.
∵CD平分∠ACB,
∴∠ACD=∠ECD.
又∵AC=CE,
CD是公共边.
∴△ACD≌△ECD.(SAS)
∴∠DEC=∠A=2∠B,DE=AD.
又∵∠DEC=∠B+∠BDE,
∴∠B=∠BDE.
∴BE=DE=AD.
∴BC=BE+EC=AD+AC.
即BC=AC+AD.
[解析] 在证明线段的和、差、倍问题时,常常用这种“截长补短”法,即在长线段上截取一段线段与其中一条短线段相等,证明剩余线段与另一条短线段相等,或在一条短线段的延长线上“补”上另一条短线段,证明新线段与长线段相等.
- 锌合金是什么意思
- 锌指结构是什么意思
- 锌氨配合物是什么意思
- 锌汞电池是什么意思
- 锌浊度试验是什么意思
- 锌版是什么意思
- 锌版画是什么意思
- 锌白是什么意思
- 锌的吸附是什么意思
- 锌的生理功用是什么意思
- 锌矿是什么意思
- 锌离子的鉴定是什么意思
- 锌筒是什么意思
- 锌粉是什么意思
- 锌缺乏症是什么意思
- 锌肥是什么意思
- 锌贸易是什么意思
- 锌钡白是什么意思
- 锌钡白颜料是什么意思
- 锌铁尖晶石是什么意思
- 锌铜石灰液是什么意思
- 锌铝合金是什么意思
- 锌银微型电池是什么意思
- 锌银蓄电池是什么意思
- 锌锰电池是什么意思
- 锌食物中毒是什么意思
- 锌食物性中毒是什么意思
- 锌黄铜的炼制是什么意思
- 锍是什么意思
- 锍幅子是什么意思
- 锎是什么意思
- 锏是什么意思
- 锏子是什么意思
- 锏床窟子是什么意思
- 锏条是什么意思
- 锏钯是什么意思
- 锏锏儿/子是什么意思
- 锐是什么意思
- 锐上是什么意思
- 锐不可当是什么意思
- 锐不可挡是什么意思
- 锐中是什么意思
- 锐俊学社是什么意思
- 锐入是什么意思
- 锐兵是什么意思
- 锐军勿攻是什么意思
- 锐减是什么意思
- 锐刀剥皮机是什么意思
- 锐刚固不磷是什么意思
- 锐利是什么意思
- 锐利勇猛,不可阻挡是什么意思
- 锐利的刀是什么意思
- 锐利的士气是什么意思
- 锐利的样子是什么意思
- 锐利的目光是什么意思
- 锐利的眼睛注视着是什么意思
- 锐利的箭是什么意思
- 锐利的鉴别力是什么意思
- 锐利的锋芒是什么意思
- 锐利而机灵的目光是什么意思