解一元一次方程的步骤

---

1．去分母：利用等式的基本性质，方程两边同时乘以各分母的最小公倍数，但要注意不要漏乘分母是1的项．

2．去括号：利用去括号法则，按先去小括号，再去中括号，最后去大括号的顺序．

3．移项：把含有未知数的项都移到方程的一边，已知项移到方程的另一边．

4．合并同类项：把未知数的系数相加，常数项相加，最终化成ax=b(a≠0)的形式．

5．系数化为1，用等式的基本性质，方程两边同时除以未知数的系数，得出方程的解x=b/a

注意 1．并不是所有的一元一次方程的解法都严格按照这一步骤顺序进行，要具体问题具体分析，并没有严格的先后，有些步骤还可能用不到．

2．解一元一次方程实质上就是利用等式的性质，进行一系列的变形，最终变成ax=b(a≠0)的形式．

3． 解方程不能连等．如：解方程x/5=3时，列成x/5=3=x=15便是错的．

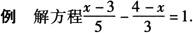
解 去分母，得3(x－3)－5(4－x)=15．

(注意：
❶ 分子加括号；
❷ 不要漏乘分母是1的项)

去括号，得3x－9－20+5x=15．

(注意：
❸ 括号前的数要乘以括号内的每一项；
❹ 括号前面是负号，去掉括号时，括号内各项都变号)

移项，得3x+5x=15+9+20．

(注意：
❺ 移项时不要漏项；
❻ 移项要变号，而在方程同一边移动项的位置时不变号)

合并同类项，得8x=44．

(注意：
❼ 按合并同类项法则进行，不要漏项)

系数化为1，得x=11/22

(注意：
❽ 正确进行运算)

[解析] 解方程时，需明确每一步在做什么变形，应该注意什么问题，同时还要从自己的错误中找原因，有针对性的纠正，不断总结经验教训．