算术平均数控制图

---

指根据样本的算术平均数(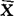)加减3个标准差(σ)制定控制界限，据此对生产过程(或工序)进行控制的一种产品质量控制图。

它是连续型随机变量计量数据的控制图。这种随机变量服从于正态分布。算术平均数控制图可以避免单值控制图中由于个别极端数值的出现而作出错误判断。

样本容量可取四个或五个，以便整除。

同时n≥4时，即使总体是非正态分布，而样本平均数的分布接近于正态分布。

中心线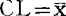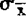为样本平均数的标准差。

数理统计证明：

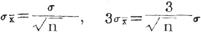
σ为总体标准差，n为样本容量。

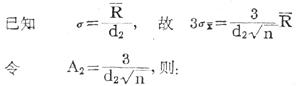
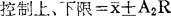
数理统计证明，样本标准差的平均数(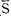)与总体标准差(σ)有如下关系：

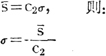
以此式代入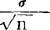，得

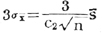
C₂为样本标准差的平均数与总体标准差之间的系数。

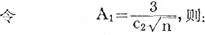
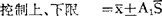
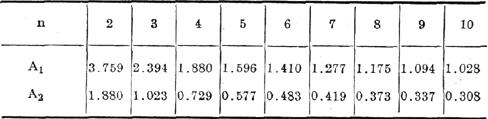
A₁与A₂数值可根据样本容量(n)查表取得。

根据正态分布理论，生产情况正常时，所抽样本平均数(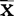)超出控制上、下限的概率只有0．003。假设超出这个界限，可认为生产过程发生了异常变化。