矩法

---

参数估计中最早引入的方法。

所谓参数估计，就是在分布函数形式已知的情况下，对决定分布函数的参数进行估计。

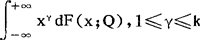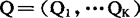设｛F(x，Q)，Q∈H｝是母体X的可能分布族，Q=(Q₁，…Q_K)是待估计的未知参数。假定母体分布的K阶矩存在，则母体的γ阶矩α_γ(Q₁，…，Q_K)=是的函数。

现取母体X的容量为n的子样X=(X₁，…，X_n)，其γ阶子样矩为。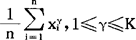

矩方法就是用子样矩作为母体矩的估计，即令

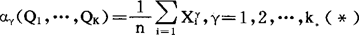这样(*)式就确定了包含K个未知参数Q=(Q₁，…Q_K)的K个方程式。解此方程组就得到Q=(Q₁，…，Q_K)的一组解。

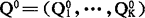由于子样矩是随机变量，所以Q·亦是随机变量。现将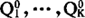分别作为Q₁，…Q_K的估计，称为矩法的估计。

这种求估计量的方法称为矩法。