相关系数

---

指两变量间线性相关程度和方向的系数。

在相关分析中，常计算相关系数来反映现象之间相关程度的大小和相关方向的正负。相关系数的计算公式为英国统计学家卡尔·皮尔生首创，故称“皮尔生系数”。这系数是依据积差计算的，又称“积矩相关系数”。

设有x、y两个相关变量，其N对资料为：(x₁，y₁)，(x₂，y₂)，……，(x_n，y_n)，则计算直线相关系数的公式为：

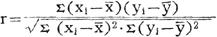
式中：r代表相关系数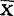，为x变量的平均数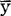，为y变量的平均数。

如果根据分组资料计算相关系数，首先要把x、y两个相关变量的实际资料进行分组，编制相关表，而后根据下列公式计算：

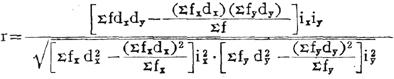
式中：f_x为x数列各变量的次数，f_y为y数列各变量的次数，i_x为x数列各组的组距，i_y为y数列各组的组距，x₀、y₀为x、y数列的假定平均数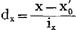为x数列的离差，d_y=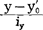为y数列的离差。

相关系数的性质是：

(1)相关系数r值所在范围为－1≤r≤+1。

(2)r为正值时，两变量间为正相关；r为负值时，两变量间为负相关。

(3)相关系数的绝对值｜r｜愈大，表示两变量间相关程度愈密切：r=+1，为完全正相关；r=－1，为完全负相关；r=0，两变量完全无关。