1.相邻元素——“捆绑法”
分两步完成:首先把相邻的元素捆在一起作为一个元素与其他元素作一次排列;再对捆在一起的元素进行排列.
例1 8个人站成一排,甲乙必须紧靠在丙的两旁,有多少种排法?
解 分两步进行:
(1)甲乙丙三人可以看成一个整体,与另外5人进行排列,有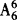 种排法;
种排法;
(2)甲乙两人的位置可以互换,有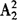 种排法(丙只能排在甲乙的中间).
种排法(丙只能排在甲乙的中间).
由乘法原理一共有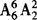 种排法.
种排法.
2.相离元素——“插空法”
分两步完成:首先将没有限制要求的元素进行排列;其次再在每两个元素间插入不能排在一起的元素.
例2 排一张包括8个节目的演出表,其中的三个小品节目不能排在一起,有多少种排法?
解 分成两步进行:
第一步:先排其他5个节目,有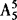 种排法;
种排法;
第二步:在排好的5个节目之间及两边有6个空位,选其中的3个位置,将三个小品节目插入,有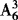 种方法.由乘法原理,有
种方法.由乘法原理,有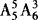 种排法.
种排法.
3.定位元素——“优先法”
首先满足特殊元素或特殊位置的要求,再考虑其他元素或位置.
例3 8个人站成两排,每排4人,其中甲必须站在前排,乙不能站在后排的边上,有多少种排法?
分析 甲、乙是特殊的元素,应首先加以考虑.
解 解法一 先排甲,有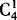 种排法.
种排法.
其次排乙,有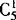 (甲排完后,乙可选前排余下的3个位置,后排中间两个位置)种排法,其余6人有
(甲排完后,乙可选前排余下的3个位置,后排中间两个位置)种排法,其余6人有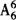 种排法.
种排法.
由乘法原理,一共有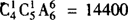 种排法.
种排法.
解法二 先排乙,分成两类:
(1)乙在前排:乙——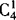 ,甲有
,甲有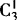 ,其他6人
,其他6人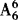 ,一共有
,一共有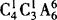 .
.
(2)乙在后排:乙——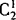 ,甲有
,甲有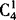 ,其他6人
,其他6人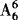 ,一共有
,一共有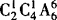 .
.
由加法原理,一共有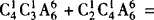 14400种.
14400种.
【说明】本题的甲、乙是特殊元素,必须做优先考虑.
4.直接求解有困难——“间接排除法”(即“正难则反”).
例4 求以一个长方体的顶点为顶点的四面体的个数.
解 长方体的8个顶点任取4个,有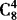 种,其中四个点共面的情况有两种:长方体的6个表面的四个顶点和6个对角面的四个顶点,因此一共有
种,其中四个点共面的情况有两种:长方体的6个表面的四个顶点和6个对角面的四个顶点,因此一共有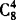 —(6+6)=58种.
—(6+6)=58种.
5.定序元素——“缩倍法”(也叫“机会均等法”)
限制某几个元素必须保持一定的顺序.
例5 10个人排成一排,
(1)甲排在乙的左边的排法有多少种;
(2)甲排在乙的左边,丙排在乙的右边的排法有多少种?
解 (1)10个人排成一排,有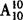 种排法,其中甲排在乙的左边与甲排在乙的右边的机会是均等的,因此有
种排法,其中甲排在乙的左边与甲排在乙的右边的机会是均等的,因此有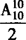 种排法.
种排法.
(2)甲乙丙三人的全排列有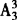 种排法,其中“甲排在乙的左边且丙排在乙的右边”只占其中的1/6,因此一共有
种排法,其中“甲排在乙的左边且丙排在乙的右边”只占其中的1/6,因此一共有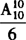 种排法.
种排法.
6.用“转化法”解题
例6 某人上楼,每一步走1个台阶或2个台阶,他一共走了8步,走了10个台阶,问:他有多少种走法?
解 此题可以转化为8步当中,哪两步走两个台阶的问题(其余6步均走一个台阶),一共有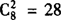 种走法.
种走法.
7.分“堆”问题——“隔板法”
解决把若干相同的元素分成若干“堆”,分配给若干人的问题.
例7 电视台把20台相同的电脑赠送给8所希望小学,每个学校至少一台,一共有多少种分法?
解 可以在20台电脑之间所形成的19个空中,插入7个“隔板”,就把20台电脑分成8份(每份至少一台),分给8所小学,一共有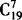 种分法.
种分法.
习题变式:求x+y+z=20的正整数解的个数.(答案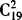 )
)
8.表格法
有些较复杂的问题用列表使其直观.
例8 9人组成篮球队,其中7人善打前锋,3人善打后卫,现从中选5人,组队出场,有多少种不同的组队方法.
解 由题设知必有一人既打前锋又打后卫,列表如下:
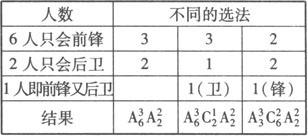
由表知,共有900种不同的方法.
- 南满铁路是什么意思
- 南滩子遗址是什么意思
- 南滩村是什么意思
- 南漒是什么意思
- 南漕海运论是什么意思
- 南漢宸是什么意思
- 南漢金石志是什么意思
- 南漪是什么意思
- 南漪堂是什么意思
- 南漪湖是什么意思
- 南漪湖风景区是什么意思
- 南漳是什么意思
- 南漳县是什么意思
- 南漳县志是什么意思
- 南漳县(城关镇)是什么意思
- 南漳子是什么意思
- 南潘村是什么意思
- 南潜是什么意思
- 南潜日记是什么意思
- 南潜集是什么意思
- 南澎岛战斗是什么意思
- 南澳县旅游局是什么意思
- 南澳县(后宅镇)是什么意思
- 南澳大利亚是什么意思
- 南澳岛是什么意思
- 南澳州立银行是什么意思
- 南澳气记是什么意思
- 南澳海岛国家森林公园是什么意思
- 南澳镇总兵是什么意思
- 南濠居士文跋是什么意思
- 南濠居士诗话是什么意思
- 南濠诗话是什么意思
- 南瀀瀀是什么意思
- 南灣子船是什么意思
- 南炕待客是什么意思
- 南点心是什么意思
- 南烛是什么意思
- 南烛叶是什么意思
- 南烛子是什么意思
- 南烛枝叶是什么意思
- 南烛草木是什么意思
- 南烧酒是什么意思
- 南無釋迦牟尼佛像是什么意思
- 南熏曲是什么意思
- 南熏門是什么意思
- 南熏门是什么意思
- 南熘八块是什么意思
- 南燕是什么意思
- 南燕世宗是什么意思
- 南燕献武帝是什么意思
- 南燕麦是什么意思
- 南燭是什么意思
- 南爵过士是什么意思
- 南牀是什么意思
- 南牀山是什么意思
- 南片白话是什么意思
- 南牌村是什么意思
- 南牙是什么意思
- 南牢记是什么意思
- 南特是什么意思