正态分布

---

亦称"高斯分布"或"拉普拉斯分布"。

其概率密度函数为

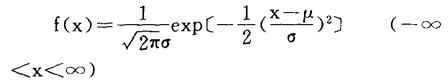
取y=f(x)作图，可描出正态分布的曲线，该曲线有下列特性：

(1)为单峰对称曲线，对称轴是x=μ；

(2)在x=μ±σ处有拐点；

(3)以全曲线与x轴所围面积等于1。该分布期望值E(x)=μ，方差D(x)=σ²，偏度γ₁=μ₃／σ³=0，峰度γ₂=μ₄／σ⁴－3=0，矩母函数M(θ)=exp(μθ+)。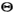

正态分布是最常见的也是最重要的一种分布。不少社会现象、自然技术现象的分布与之相近。

在一般假定下，它是n个独立随机变量之和且当n充分大时的极限分布。