极大似然估计

---

以似然原则为基础的估计方法，是最常用的一种估计方法。

设总体x有分布密度p(x|θ)，其中，θ=(θ₁，…θ_m)是m维待估计的未知参数。设x_i=x_i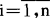，，是来自总体X的容量为n的随机独立样本。则x₁，…，x_n的联合分布密度在点(x₁，…，x_n)处的值为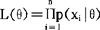(如果总体x的分布是离散的，将式子右端的因子p(x_j|θ)理解为P｛X_i=x_i|θ｝，极大似然估计法可照样使用)。θ的值应有利于样本值(x₁，…，x_n)的出现，也就是使得L(θ)达到极大值。这就是似然原则。函数L(θ)称作似然函数。

因此，求极大似然估计实际上就是求似然函数L(θ)的极大值点。由于对数函数的严格单调性，L(θ)与1ogL(θ)同时达到极大值，而求1ogL(θ)的极值点比较方便。故可转化为求logL(θ)的极大值点。

利用极值的必要条件可以得到下面的方程组：

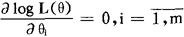
(1)称作似然方程组。如果由(1)解出的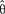确实使logL(θ)，从而也使L(θ)达到极大值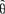，就叫做未知参数θ的极大似然估计。θ的函数g(θ)的极大似然估计为。

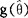例如，设总体分布为N(μ，σ²)，其中μ，σ²是未知参数，得到了容量为n的样本X_i=x_i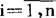，。则μ及σ²的极大似然估计可以由下面步骤得到：

(i)构造似然函数

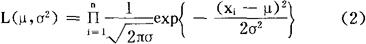
(ji)写出似然方程组

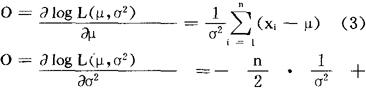
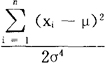
(iii)求解(3)，得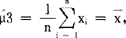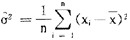，，可以验证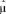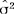，确实是logL(μ，σ²)的极大值点，因而它们分别是μ和σ²的极大似然估计。

极大似然估计有许多优良的大样本性质，如相容性、渐近正态性、渐近有效性等。但是以下几个问题应予注意：极大似然估计有时不存在；有时不唯一；当参数数目随n趋于无穷时，极大似然估计不一定具有好的性质，例如，设X_ij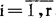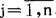，，，服从分布N(μ₁，σ²)，相互独立，则当r→∞时，σ²的极大似然估计不是相容估计量(详尽的讨论见Neyman dScott，1948，Econometrica，16，1－32，以及Keifer d Wolfowitz，1956，Ann·Math．statist．27，887－906)