无理数的估算

---

对无理数的估算主要是估计它在哪两个有理数之间．估算并不要求十分精确，只需求出一个大致的范围即可．

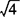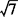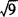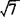注意 1．估算方法：一般根据乘方运算和开方运算的互逆关系，可以寻找乘方前结果最接近于被开方数的两个有理数，从而确定某个数的大致范围．如<<，即2<<3．可知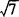的整数部分是2．

2．可以通过无理数的估算比较两个无理数的大小，或一个无理数与一个有理数的大小．

例1 5+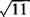的小数部分为a，5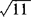－的小数部分为b，求a+b的值．

解 ∵3<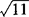<4，

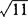∴的整数部分是3．

∴5+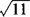的整数部分是8，小数部分a=．

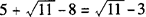5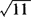－的整数部分是1，小数部分b=．

∴．

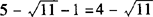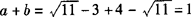例2 下图是某校园内的一块长方形绿地，已知绿地长AB=40m，宽BC=20m．

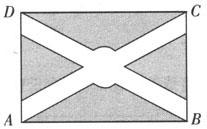
(1)中间连接相对两角的小路AC长多少?它有60m吗?

(2)如果要求误差小于1m，中间小路AC长大约是多少?

(3)学校准备在这块绿地中央修建一个圆形喷水池，它的面积是300m²，你能估计它的半径吗?(误差小于1m)

解 (1)．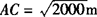

因为60²=3600，远远大于2000，所以AC长没有60m

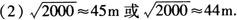
(3)设喷水池的半径为Rm，依题意得：πR²=300．

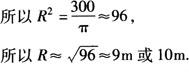
所以喷水池的半径为9m或10m．