效用函数决策法

---

指在风险型决策问题中，事实上选择的往往不是最大期望利润的方案，而往往依据著一种确实存在的非线性效用函数来进行决策的方法。

例如有下列带风险型的决策矩阵提供给决策者：

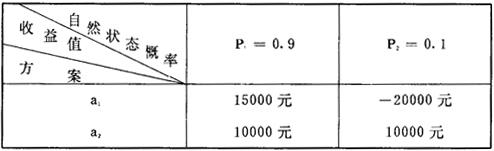
按最大期望利润选择原则

E(a₁)=(0．9)×(15000)+(0．1)×(－20000)

=11500(元)

E(a₂)=(0．9)×(10000)+(0．1)×(10000)

=10000(元)

应选择a₁方案。但实际上许多决策者宁肯选择10000之期望利润的a₂方案，而不愿选择11500之期望利润的a₁方案。这表明对决策者而言存在著非线性的效用函数。

效用函数决策法的计算公式及程序是：

❶ 依据决策矩阵表中的收益值，明确效用尺度(0～1)，建立效用曲线，求出收益值V_ij的对应效用值X_ij。

例如上例效用曲线图如下Ca₂bd表示，各肯定的收益值可在Ca₂bd

曲线上交点的纵坐标上读出相应的效用值。

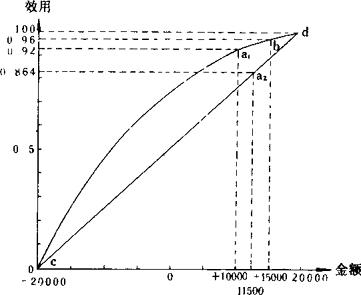
❷ 用效用值X_ij代替V_ij，建立效用值决策矩阵例。

❸ 计算期望效用，并选取期望效用大的方案为决策方案。

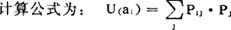
U(a₁)=(0．96×0．9)+(0×0．1)=0．864

上例

U(a₂)=(0．92×0．9)+(0．92×0．1)=0．92

故按效用函数决策法应选取a₂方案。