已知末端装置的微运动dD,需求各关节产生该微运动的微变化dq时,可按下式计算:
dq=J-1dD (5.13-60)
当行列式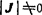 ,则逆矩阵J-1存在。当|J|=0时,J-1不存在,这时操作手的位形称为奇异位形。奇异位形时,通常是二个或n个关节轴共线,因此有一个关节或n个关节不起作用,操作手自由度缩减了,因此也可称为操作手退化。这时可把多余的共线关节锁住,全部运动由一个关节来完成。
,则逆矩阵J-1存在。当|J|=0时,J-1不存在,这时操作手的位形称为奇异位形。奇异位形时,通常是二个或n个关节轴共线,因此有一个关节或n个关节不起作用,操作手自由度缩减了,因此也可称为操作手退化。这时可把多余的共线关节锁住,全部运动由一个关节来完成。
由于操作手雅可比矩阵J是-6×6矩阵,因此直接用矩阵代数求J-1的计算量太大。为此,出现有各种方法求微运动的逆关系式。例如,对(5.13-26)第三式,即对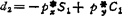 微分,得
微分,得
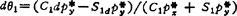
依次类推。如果能求得形式简单的'J,则可直接从4J求逆微分关系式。这是最简捷的方法。
从(5.13-59)式第二个方程:θ2=4vy/a2C3。当C3=0时为奇异位形。
以S4乘第一式,C4乘第三式,二式相减,得θ1=(S44vx-C44vz)/(a2C2-S23d4)。当a2C2-S23d4=0时为奇异位形,此时W点位于第一关节轴上。
以C4乘第一式,S4乘第三式,二式相加,得θ23=-(C44vx+S44ba-S3a2θ2)/d4。
从第四式得:θ6=(S23C4θ1-S4θ23-4Ωx)/S5。当S5=0时为奇异位形。
从第五式和第六式得:θ4=4Ωy-C23θ1-C5θ6;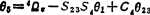 。
。
- 寇敌是什么意思
- 寇昏以狂,敢蹈愬疆。是什么意思
- 寇松是什么意思
- 寇松线是什么意思
- 寇梦碧是什么意思
- 寇氏是什么意思
- 寇氏全幼心鉴是什么意思
- 寇氏法是什么意思
- 寇氛是什么意思
- 寇水娃是什么意思
- 寇永安是什么意思
- 寇治墓志是什么意思
- 寇泚是什么意思
- 寇洛是什么意思
- 寇湄是什么意思
- 寇湘是什么意思
- 寇準是什么意思
- 寇準·江南春二首(其二)是什么意思
- 寇演墓志是什么意思
- 寇漫汗国是什么意思
- 寇热是什么意思
- 寇烽是什么意思
- 寇犁等行窃案是什么意思
- 寇瑊招募“白艻子兵”是什么意思
- 寇瑜是什么意思
- 寇略是什么意思
- 寇盗是什么意思
- 寇盗方归顺,乾坤欲晏如。是什么意思
- 寇窃是什么意思
- 寇能往,我亦能往是什么意思
- 寇脱是什么意思
- 寇至,则先去以为民望。是什么意思
- 寇臻墓志是什么意思
- 寇英傑是什么意思
- 寇英杰是什么意思
- 寇荣被诬陷案是什么意思
- 寇莫汗国是什么意思
- 寇莱公思亲罢宴是什么意思
- 寇莱公集是什么意思
- 寇虏是什么意思
- 寇衡全幼心鉴是什么意思
- 寇謙之是什么意思
- 寇警是什么意思
- 寇谦之是什么意思
- 寇谦之楷书中岳嵩高灵庙碑是什么意思
- 寇谦之的人物故事|评价|小传,寇谦之的事迹|史鉴是什么意思
- 寇贞莲是什么意思
- 寇贼是什么意思
- 寇贼充斥是什么意思
- 寇贼奸宄是什么意思
- 寇贾是什么意思
- 寇贾辅汉是什么意思
- 寇赞是什么意思
- 寇边是什么意思
- 寇连材是什么意思
- 寇述彭是什么意思
- 寇遐是什么意思
- 寇钞是什么意思
- 寇雉是什么意思
- 寇雠是什么意思