15.3.1 均差插值公式
插值点为x0<x1<…<xn,
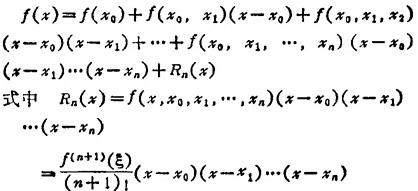
(ξ在x0,xn和x中的最小值与最大值之间)。
15.3.2 拉格朗日插值公式
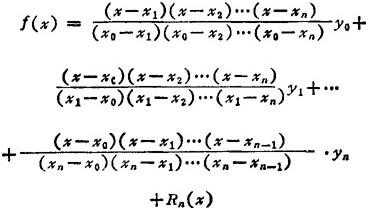
式中 Rn与15.3.1中Rn相同。
15.3.3 牛顿向前插值公式
适用于x接近a而大于a的情况。插值点为x0=a,x1=a+h,…,xn=a+nh。
f(x)=f(a+th)=y0+t△y0+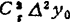 +…+
+…+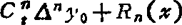
式中
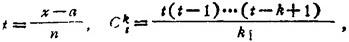
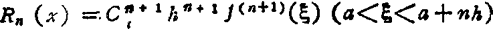
15.3.4 牛顿向后插值公式
适用于x接近于a而小于a的情况,插值点为
x-n=a-nh,x-(n-1)=a-(n-1)h,…x-1=ah,x0=a0
f(x)=f(a-th)=y0-t▽y0+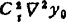 -…+(-1)“
-…+(-1)“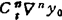 +Rn(x)
+Rn(x)
式中 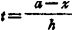 ;
;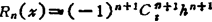 f)n+1)(ξ),(a-nh<ξ<a)。
f)n+1)(ξ),(a-nh<ξ<a)。
15.3.5 三次样条插值函数
插值点为x0<x1<…<xn。区间〔x0,xn〕上y=f(x)的三次样条插值函数S(x)指的是满足下列三个条件的函数:1.在每一子区间〔xj,xj+1〕上S
(x)都是三次多项式;2.S(xj)=f(xj)=yj,(j=0,1,2,…n),3.在〔x0,xn〕上S(x)有一至二阶连续导数(曲线光滑连接)。则在子区间〔xj,xj+1〕(j=0,1,2,…,n-1)上
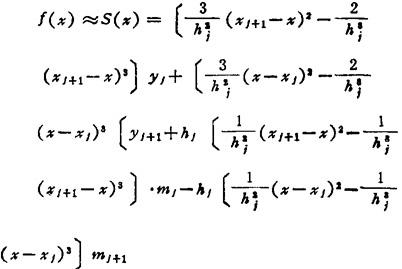
式中 hj=xj+1-xj;mj=S′(xj)由下列方程组及其边界条件确定:
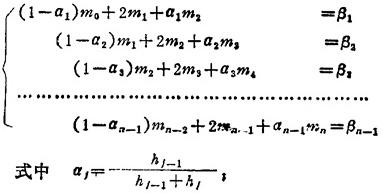
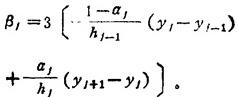
常见的几种边界条件为:
❶ 已知S′(x0)=m0,S′(xn)=mn
❷ 已知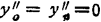 ,
,
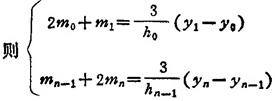
❸ y=f(x)为周期函数,其基本周期为xn-x0,
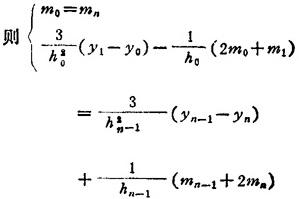
- 史荫绵是什么意思
- 史药房是什么意思
- 史華是什么意思
- 史萃是什么意思
- 史葉是什么意思
- 史蒂文斯是什么意思
- 史蒂文斯定律是什么意思
- 史蒂文斯,d.是什么意思
- 史蒂文斯,h.h.是什么意思
- 史蒂文斯,s.m.是什么意思
- 史蒂文斯,华莱士是什么意思
- 史蒂文斯,埃德温·奥古斯塔斯是什么意思
- 史蒂文斯,撒迪厄斯是什么意思
- 史蒂文斯,约翰是什么意思
- 史蒂文斯,西奥多·富尔顿是什么意思
- 史蒂文森是什么意思
- 史蒂文森第二是什么意思
- 史蒂文森,艾德莱·尤因是什么意思
- 史蒂文,d. a.是什么意思
- 史蒂芬森是什么意思
- 史蒂芬逊是什么意思
- 史蔚复是什么意思
- 史蔚馥是什么意思
- 史蕉饮是什么意思
- 史虚白是什么意思
- 史蜀君是什么意思
- 史蜀胡悉是什么意思
- 史行是什么意思
- 史裁是什么意思
- 史西村是什么意思
- 史要编是什么意思
- 史见是什么意思
- 史角是什么意思
- 史觿是什么意思
- 史詠赓是什么意思
- 史詩老墓志是什么意思
- 史譯宣是什么意思
- 史计栋是什么意思
- 史记是什么意思
- 史记·万石张叔列传第四十三 - 万石君名奋,其父赵人也,姓石氏。是什么意思
- 史记·万石张叔列传第四十三 - 万石君少子庆为太仆,御出,上问车中几马,庆以策数马毕,举手曰:是什么意思
- 史记·万石张叔列传第四十三 - 塞侯直不疑者,南阳人也。是什么意思
- 史记·万石张叔列传第四十三 - 太史公曰:是什么意思
- 史记·万石张叔列传第四十三 - 建元二年,郎中令王臧以文学获罪。是什么意思
- 史记·万石张叔列传第四十三 - 建陵侯卫绾者,代大陵人也。是什么意思
- 史记·万石张叔列传第四十三 - 御史大夫张叔者,名欧,安丘侯说之庶子也。是什么意思
- 史记·万石张叔列传第四十三 - 郎中令周文者,名仁,其先故任城人也。是什么意思
- 史记·三代世表第一是什么意思
- 史记·三王世家第三十 - “大司马臣去病昧死再拜上疏皇帝陛下:是什么意思
- 史记·三王世家第三十 - “维六年四月乙巳,皇帝使御史大夫汤庙立子闳为齐王。是什么意思
- 史记·三王世家第三十 - 太史公曰:是什么意思
- 史记·三王世家第三十 - 夫广陵在吴越之地,其民精而轻,故诫之曰是什么意思
- 史记·三王世家第三十 - 燕土埆,北迫匈奴,其人民勇而少虑,故诫之曰是什么意思
- 史记·三王世家第三十 - 王夫人者,赵人也,与卫夫人并幸武帝,而生子闳。是什么意思
- 史记·三王世家第三十 - 褚先生曰:臣幸得以文学为侍郎,好览观太史公之列传。是什么意思
- 史记·东越是什么意思
- 史记·东越列传第五十四 - 太史公曰:是什么意思
- 史记·东越列传第五十四 - 至元鼎五年,南越反,东越王馀善上书,请以卒八千人从楼船将军击吕嘉等。是什么意思
- 史记·东越列传第五十四 - 闽越王无诸及越东海王摇者,其先皆越王勾践之后也,姓驺氏。是什么意思
- 史记·乐书是什么意思