如果a1,a2,…,an∈R+,且n>1,则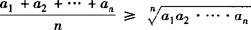 ((当且仅当a1=a2=…=an时取“=”号).
((当且仅当a1=a2=…=an时取“=”号).
例1 已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( ).
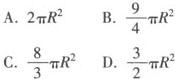
分析 本题考查了圆锥与圆柱的基本计算,同时考查了利用均值不等式求最值.
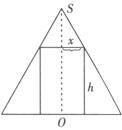
解 如图作圆锥的轴截面图,设内接圆柱的底面半径为x,高为h,则由三角形相似可得:
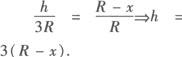
∴圆柱的全面积为:
S全=2πxh+2πx2
=2πx·3(R—x)+2πx2
=2πx(3R—2x)
=π·2x(3R—2x)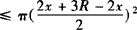
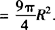 .
.
当且仅当2x=3R—2x即x=3/4R时取“=”号,故选B.
评析 本题也可用二次函数求最值
例2 a>b>1,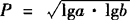 ,Q=1/2(1ga+lgb),
,Q=1/2(1ga+lgb),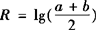 ,则( ).
,则( ).
A.R C.Q 分析 本题考查了对数的基本性质及均值不等式的应用. 故R>Q,从而选B. 评析 本题也可用特殊值法来判定,如果a=100,b=10,很容易选B,解这类题要善于利用特例法求解,利用均值不等式和函数单调性比较大小是常用的方法. 例3 设x、y、z为正数,x2+y2+z2=1,试求 解 若a、b、c∈R+,则由平均值不等式可知:a2+b2+c2≥ab+bc+ca∴(a+b+c)2≥3(ab+bc+ca), 当且仅当x=y=z时取得最小值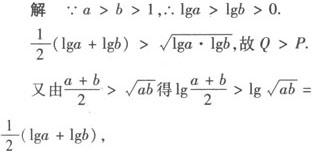
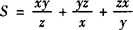 的最小值.
的最小值.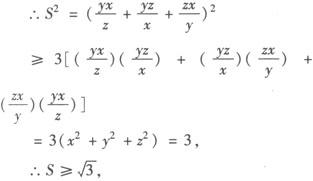
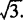 .
.
- 半枫荷根是什么意思
- 半枫荷根是什么意思
- 半枫荷药酒是什么意思
- 半格律诗是什么意思
- 半格诗是什么意思
- 半横向通风是什么意思
- 半死是什么意思
- 半死不活是什么意思
- 半死不活是什么意思
- 半死半生是什么意思
- 半死桐(半死心、半死龙门树)是什么意思
- 半殖民地是什么意思
- 半殖民地是什么意思
- 半殖民地是什么意思
- 半殖民地半封建国家是什么意思
- 半殖民地半封建国家是什么意思
- 半殖民地半封建性市场是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会是什么意思
- 半殖民地半封建社会的主要矛盾是什么意思
- 半殖民地半封建社会的形成是什么意思
- 半殖民地半封建社会的特点是什么意思
- 半毡是什么意思
- 半水浮沉难得地,清流砥柱不沾泥。是什么意思
- 半江瑟瑟半江红是什么意思
- 半济而击之是什么意思
- 半浮动筏式养殖是什么意思
- 半涂是什么意思
- 半涂而废是什么意思
- 半淞园路是什么意思
- 半深海沉积是什么意思
- 半深海沉积是什么意思
- 半温半热汤是什么意思
- 半温半热汤是什么意思
- 半滑舌鳎是什么意思
- 半潜式海上石油钻井平台是什么意思
- 半潜式钻井装置是什么意思
- 半潜驳是什么意思
- 半点是什么意思
- 半照是什么意思
- 半牀是什么意思
- 半独立式动力输出轴是什么意思
- 半环扁尾蛇毒素是什么意思
- 半琥泊酸泼尼松龙是什么意思
- 半琥珀酸丁酰胺是什么意思
- 半琥珀酸布酰胺是什么意思
- 半瓶子醋好晃荡是什么意思
- 半瓶醋是什么意思
- 半生是什么意思
- 半生半熟是什么意思
- 半白是什么意思
- 半知菌亚门是什么意思
- 半砖,封口[堵头,封缝]砖是什么意思
- 半硫丸是什么意思
- 半硫丸是什么意思
- 半硫丸是什么意思