指数函数的图象及性质

---

例1 (1)比较(0．034)^—0001与634^—01的大小；

(2)若a=0．2^—3/4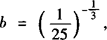，，c=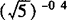，则a，b，c的顺序关系如何?

解 (1)由指数函数的性质知(0．034)^—0001>1，634^—0．1<1，所以(0．034)^—0001>634^—01．

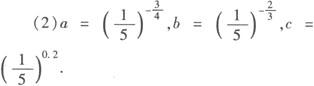
因为0<1/5<1，可知函数y=(1/5)^x是减函数，0．2>—2/3>—3/4．

所以a>b>c．

例2 求下列函数的值域及单调区间

❶ ；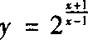

❷ y=(1/3)^x2—2x—3．

解 ❶ 由x—1≠0得函数的定义域为{x|x∈R且x≠1}．

设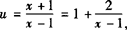，则u∈R且u≠1．

∴函数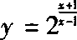的值域为{y|y>0且y≠2

∵x∈(—∞，1)时，u为减函数，

x∈∈(1，+∞)时，u为减函数，

又∵y=2^x为增函数，

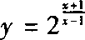∴在(—∞，1)、(1，+∞)上都是减函数．

❷ 函数的定义域为R．

设u=x²—2x—3=(x—1)²—4≥—4．

∴0—4=81，

即函数的值域为{y|0

∵x∈(—∞，1]时，u为减函数，

x∈[1，+∞)时，u为增函数，

又∵ y=(1/3)^x为减函数，

．．y=(1/3)^x2—2x—3的减区间为[1，+∞)增区间为(—∞，1]．