异面直线的判定定理

---

过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线．

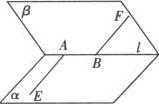
例 如图，已知α∩β=l，A∈l，B∈l，且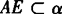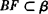，求证：AE和BF是异面直线．

策略 证明两条直线是异面直线，通常用反证法．

证明 假设AE和BF共面，因为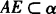，B∈α，且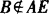，所以过AE及点B有且只有一个平面α，因此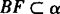，这就与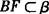且α∩β=l相矛盾，故AE和BF是异面直线．

点评 用反证法证a、b是异面直线，有时要否定a∥b及a∩b=A两种情况，本例是直接否定a、b共面，反证法是一种十分重要的方法，在立体几何中有著广泛的应用，熟练地掌握和运用反证法是学习立体几何的必备基础之一，反证法证明的一般步骤为(1)反设；(2)归谬；(3)结论．