常态分布

---

又名正态分布。

指连续变量的统计总体中的各个体的分布，呈现同其平均值密集成两边对称的形态，是数理统计中最重要的连续型分布。其特征是：(1)各个体大小与其平均数的小误差，比其大误差多。(2)很大的误差不至发生。(3)同值的正误差与其负误差彼此相消，分配为对称。

若随机变量Z的分布密度f(x)为：

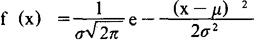
(－∞＜x＜∞)

则称随机变量Z服从参数为μσ²的正态分布N(μ、σ²) (σ＞0，－∞＜μ＜+∞)

当μ=0 σ=1时，分布密度函数以Φ(x)表示。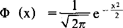(平均数差为原点)

标准式中：

Φ(x)为标准常态密度；

π为圆周率；

e为自然对数之底。

一般常态分布密度函数的图形为：

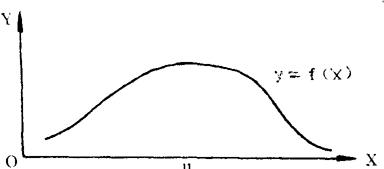
由图可知，正态分布密度函数的图形是中间高，两边低，以横坐标为渐近线的曲线。