双变量回归模型

---

指包含有一个应变量和一个自变量的回归模型。

将自变量与应变量合在一起称两个变量，是计量经济学中特有的说法。由于模型通常是线性的，所以也有人意译为“一元线性回归模型”或“简单线性回归模型”。

其线性模型的一般形式如下：

Y_i=β₀+β₁X_i+u_i

i=1，2，…，n

此处Y为应变量(或被解释变量)，X为自变量(或解释变量)，u为随机扰动项，β₀与β₁为待定参数。

如果模型符合经典线性回归模型的假定，那么可以用普通[最小二乘法]计算出β₀与β₁的估计值

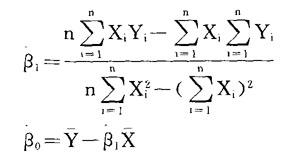
此处Y为Y的平均值，X为X的平均值。

经过参数的[假设检验]，如果β₀与β₁被接受，那么模型

Y_i=β₀+β₁X_i

可以认为初步成立。但是要成为正式使用的模型，还需要经过经济学的检验、计量经济学的检验和其他统计检验。

对于违反经典线性回归模型假定的情况，参见[最小二乘法]中广义最小二乘法部分。

非线性模型的处理方法参见[多变量回归模型]。