厄密特－费叶插值理论

---

设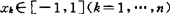为一节点系，f(x)为定义在［－1，1］上的实函数。

称满足

H_n(f，x_k)=f(x_k)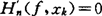，，k=1，…，n (1)

的2n－1次代数多项式H_n(f，x)为函数f(x)的厄密特－费叶插值(多项式)(以下简记HF插值)。取雅可比(Jacobi)多项式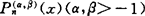的零点为节点系，记对应的HF插值多项式为。

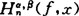以第一类和第二类契比晓夫(Chebyshev)多项式T_n(x)，U_n(x)的零点为节点系的HF插值分别是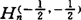(f，x)和。

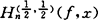此外，对条件(1)进行修改还有拟厄密特－费叶插值和高阶厄密特－费叶插值。

一方面，由于HF插值构造简单，且对不同节点系具有不同的性质；另一方面，由于它与计算有关和在理论上的价值，使得对这类插值的研究成果较多。主要分为以下3个方向：

1．逼近阶的估计。

1916年，费叶(L．Fejér)证明，对于f∈C［－1，1］

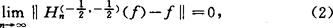
这里‖·‖表示在［－1，1］上的一致范数。

以后，波波维奇(T．Popoviciu)等人建立了用连续模估计(2)的逼近阶。

其中较好的结果是鲍亚尼奇(R．Bojanic)于1969年建立的第1个非点态精确逼近阶：

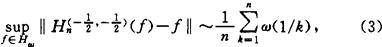
此处和以后，记号“A_n～B_n”表示存在两常数0＜C₁＜C₂使C₁A，，≤B_n≤C₂A_n；

H_ω=｛f∈C［－1，1］；ω(f，t)=0(ω(t))｝，ω(t)是给定的连续模。

1981年，谢庭藩和哥德诺夫(S．J．Goodenough)等人各自独立地建立了体现(1)的插值性质的点态逼近阶：

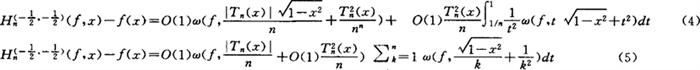
精确的点态阶是什么呢?这是沈燮昌在1983年提出的1个问题。1984年，孙燮华解决了这个问题，建立了下述的点态精确阶：

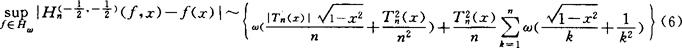
不难验证(4)与(6)的右边是等价的。因此，谢庭藩给出的估计(4)是精确的。

其实，(6)的第一个点态精确阶是孙燮华对拟HF插值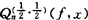于1983年建立的。沿著这个方向，1984年谢庭藩对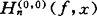建立了点态精确阶，解决了沈燮昌于1983年提出的另一问题。随后，1986年孙燮华对一切－1＜α，β≤0建立了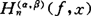的点态精确阶。但是，所有这些结果都是对正的HF插值建立的。

对于非正的HF的插值，比如，对于较简单的关于契比晓夫节点的拟HF插值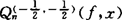能否建立形如(6)，或者较弱的结果(3)的问题尚未解决。就逼近阶估计这个方向而言，虽然今后的研究热点是对雅可比节点以外的其它各种节点，比如，拉盖尔(Laguerre)节点，厄密特节点、其它正交多项式的零点为节点的HF插值，高阶HF插值建立逼近阶的估计，但是，重要的进展将是对非正的HF插值建立点态的精确阶。

2．逼近阶的渐近展开。1981年，哥德诺夫等人对拟HF插值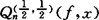建立了点态渐近展开式

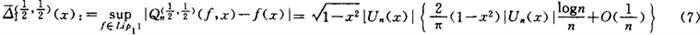
同年，蒋元林对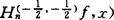建立了非点态的渐近式

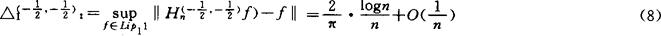
他的结果(8)被孙燮华改进为点态的渐近式。

同时，首次建立了对Lip1α(0＜α＜1)类的渐近展开式。

1985年，哥德诺夫对偶数的n建立了非点态的完全的渐近式

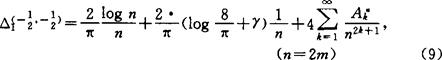
此处γ是欧拉(Euler)常数，B_2k(k=1，2，…)是贝努里(Bernoulli)数，

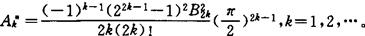
1990年，蒋元林又将(9)改进为点态渐近式。对于奇数n，相应的完全展开式是什么呢?这是一个有意义的问题。对于Lip₁α(0＜α＜1)的渐近展开问题可能更困难些，但是，这些问题的解决正是这个方向的有价值的重要进展。

1985年，谢庭藩注意到(7)式中，当x趋向于端点±1和节点x_k时，展开式的主项的阶将高于余项。也就是说，(7)式是非一致成立的。于是，谢建立了第1个一致成立的渐近式：

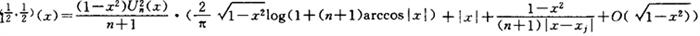
式中x_j为最接近x的一个节点。

对于一般的雅可比节点，由于它不能通过三角替换变成［0，π］上的等距节点，所以这类问题要开辟新方法。

谢庭藩问

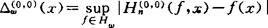
有怎样的渐近式?

1986年，周信龙先建立叶菲莫夫(Efimov)型渐近展开，然后解决了上述问题中ω(t)=t的情形。对于一般情形，甚至对ω(t)=t^σ(0＜α＜1)情形，问题尚未解决。

同前节的问题一样，所有上述的结果都是对正的HF插值建立的。今后，若能对非正的HF插值建立渐近式将是这个方向上的另一重要成果。

3．饱和问题与逆定理。德伏(R．A．DeVore)曾经提出算了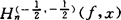的饱和问题，这个问题，在1973年被沙巴陶斯(J．Szabados)解决。他证明：

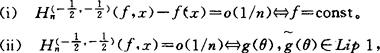
此处g(θ)=f(cosθ)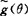，是g(θ)的共轭函数。

对于一般Jacobi节点，相应插值的饱和问题较困难。

1985年，周信龙在这方面取得重要进展，解决了当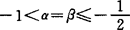时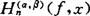，的饱和问题：

(i)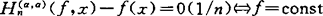 (10)

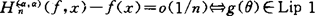(ii)且

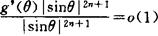
1987年，他进一步解决了当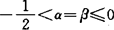时相应的饱和问题。此外，周信龙还首选建立了点态饱和定理，即(10)中的阶代之以点态阶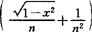，从而建立相应的充要条件。

与饱和问题密切相关的是正逆定理的建立。谢庭藩于1981年建立了如下正逆定理：设ψ(δ)＞0(0＜δ≤1)是单调增函数，满足

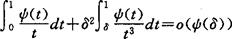
则

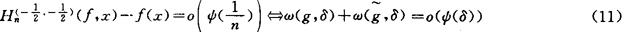
显然，除(11)外，大量的逆定理问题都未解决，还有点态正逆定理、非正的HF插值的饱和与正逆定理也都是今后值得研究的有意义的问题。

。【参考文献】：

1 谢庭藩．数学年刊，1981，2：463～472

2 Goodenough S J，et a1．J Approx．Theory，1981，31：253～260

3 沈燮昌．数学进展，1983，31，253～260

4 孙燮华．高等学校计算数学学报，1983，5：366～373

5 Xie Tingfang Chin．Ann Math，1985，6B；457～464

6 Zhou Xinlong．Approxi Th its Appl，1985，1：17～26

(中国计量学院孙燮华教授撰)