区间动力系统的强健稳定性

---

强健性是近年来许多数学分支的热门话题。

所谓强健性，常常可以定义为一个动力系统的某些固有性质在特定的结构扰动下的不变性。李雅普诺夫(Liapunov)意义下的强健稳定性便是一个动力系统在指定的结构扰动下的不变的李雅普诺夫稳定性。这类问题有很强的实际背景，因为数学模型描述一个实际动态过程每每是近似的，或因测量与计算的误差，或为了必要的简化，常有建模误差以及随环境变化的参数扰动，故研究实际问题时对一个不确定动力系统(或微分包含，或多值微分方程)的强健行为比对一个确定性系统的灵敏的定性性质更有兴趣。

李雅普诺夫意义下的强健稳定性主要研究以下两方面的问题：

1．给定一个动力系统及它的参数变化范围(一般为区间)，研究该系统在允许的参数扰动下的稳定性，例如：研究微分包含：

自然要研究区间矩阵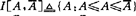的H，S稳定性，这里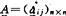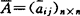，已知，A(a_ij)_n×n不确切知道，仅知。

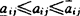令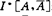表由端点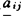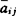，_，i，j=1，2，…，n组成的矩阵全体，显然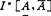有无穷多个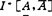，最多有2ⁿ²个。

有人著文断言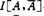与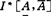的H稳定性等价，S稳定性等价，但随后就有人举反例否定这些结论，且指出其证明错在何处。

到目前还只得到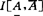为H稳定，S稳定的一些充分条件。充要条件是什么，至今未知。

对于H矩阵，S矩阵同样有人研究H稳定的强健度，5稳定的强健度，也同样有人研究其多胞形的H稳定性，S稳定性，其方法大多数是用李雅普诺夫函数或矩阵特征值估计法。

将这些思想推广到时滞系统、中立型系统，也有不少类似的工作。

从稳定性理论的发展史可看到，人们早就注意到了研究始值与系统的结构同时扰动下的稳定性(即经常干扰下的稳定性)比李雅普诺夫稳定性更有意义，它与今天的强健稳定性类似。为何前者已少有人问津，后者则成为热门话题?因为在很一般的条件下，经常干扰下的稳定性与李雅普诺夫一致渐近稳定性等价。

此外，经常干扰下的稳定性定义中的两个扰动区域只求存在，不计大小，而实际问题中，要求扰动区域为额定。拉萨尔(Lasalie)和莱夫赫茨(Lefschitz)提出了实用稳定性概念，更接近于现在的强健稳定性，但在一段相当长时间内响应者很少，固然是由于提法过于一般，更重要的是未得到更多的实际问题的支持。

最近，拉克什米堪森(Lakshmkantham)等人重新提出实用稳定性，将拉萨尔等人的实用稳定性定义的两个集合予以量化，随后写了一本书。

系统的所谓关联稳定性，非减性控制系统的绝对稳定性等等都可视为强健稳定性的雏型。

从已有的论文看，除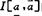的H稳定研究彻底外，其它方面则尚逊色，已有的结果，或条件太复杂，或结果较保守。如何克服条件的复杂性及降低结果的保守性，恐怕还有很多工作可做。

强健性概念还可期望推广到其它领域，如生态系统、神经网络系统、常微结构稳定性，甚至在偏微分方程、偏泛函微分方程、随机微分方程中引述强健度，也不无意义。

。

【参考文献】：

1 Lasalle J, Lefschtz S. Stability by Liapunov's Direct Method with Applications, New York: Academic Press, 1961

2 Khartionov V L. Differentialnye Uravneniya ,14(11)

3 YeungKS. Int J Control,1983,38(2) :459～464

4 Barmish B R. IEEE Transaction on Automatic Control,1984,29(10):935～946

5 Hoklot C C, Bartlet A. IEEE Transaction on Automatic Control,1986,31(1) ,355～357

6 Yerry K S, Wang S S. IEEE Transaction on Automatic Control ,1987,32(9) ,818～823

7 Aderson B D O, Jury E L. IEEE Transaction on Automatic Control,1987,32(10):909～913

8 Huang L. Hollot C V, Batlett C. Int J. Control, 1987,45 (2):649～660

9 Ciesik J N. IEEE Transaction on Automatic Control, 1987, 32(3):237～238

10 Lakshmikantham V, Leela S, Martynyuk A A. Stability Analysis of Nonlinear Systems, New York and Basel par-cel DekkerInc,1989

(华中师范大学廖晓昕教授撰)