高斯消去法
指解线性方程组的一般方法。它使线性方程组的求解问题得以彻底解决,并由于有明确的程序,因而是使用电子计算机解线性方程组常用的一种方法。
运用高斯消去法的基本要求是:①明确高斯消去法的思想是顺序消元。②懂得线性方程组的初等变换(交换两个方程的位置;用一个非零数乘以某一方程的两边;把一个方程的两边乘以同一个数,再分别加到另一个方程的两边上去)均为同解变换。③熟练掌握解n个未知量、m个方程的线性方程组的一般步骤,明确关键是施行初等变换,把方程组化为阶梯形,并能据此对解的情形进行讨论:在最后一个含有非零系数(包括常数项)的方程中,若至少有一个未知数的系数不为零,则方程组有解,否则无解。在有解时,若未知量的个数等于阶梯形方程组中方程的个数,则有唯一解;未知量的个数多于方程的个数,则有无穷多解。还要能熟练求出一般解:把每个方程中第一个有非零系数的项留在方程左边,其余未知量移到方程右边,作为自由未知量,最后要自下而上逐次代入,求得线性方程组的一般解。④能分离系数,以矩阵为工具,运用高斯消去法:对线性方程组的增广矩阵施行行的初等变换,(相等于线性方程组的初等变换),把它化为阶梯形矩阵(元素全为零的行在下方,非零行中,第一个不为零的元素的列标随着行标的增大而严格增大),此时,非零行的行数即增广矩阵的秩。划去最后一列后,其非零行行数即系数矩阵A的秩。 若秩=秩A,则线性方程组有解,否则无解。有解时,若秩A=n,则有唯一解;若秩A 需要注意的是:①只能对增广矩阵施行行的初等变换。②要选择尽量简便的初等变换,尽可能避免出现分数,在无法避免时,要使之尽可能迟出现。
运用高斯消去法的基本要求是:①明确高斯消去法的思想是顺序消元。②懂得线性方程组的初等变换(交换两个方程的位置;用一个非零数乘以某一方程的两边;把一个方程的两边乘以同一个数,再分别加到另一个方程的两边上去)均为同解变换。③熟练掌握解n个未知量、m个方程的线性方程组的一般步骤,明确关键是施行初等变换,把方程组化为阶梯形,并能据此对解的情形进行讨论:在最后一个含有非零系数(包括常数项)的方程中,若至少有一个未知数的系数不为零,则方程组有解,否则无解。在有解时,若未知量的个数等于阶梯形方程组中方程的个数,则有唯一解;未知量的个数多于方程的个数,则有无穷多解。还要能熟练求出一般解:把每个方程中第一个有非零系数的项留在方程左边,其余未知量移到方程右边,作为自由未知量,最后要自下而上逐次代入,求得线性方程组的一般解。④能分离系数,以矩阵为工具,运用高斯消去法:对线性方程组的增广矩阵施行行的初等变换,(相等于线性方程组的初等变换),把它化为阶梯形矩阵(元素全为零的行在下方,非零行中,第一个不为零的元素的列标随着行标的增大而严格增大),此时,非零行的行数即增广矩阵的秩。划去最后一列后,其非零行行数即系数矩阵A的秩。 若秩=秩A,则线性方程组有解,否则无解。有解时,若秩A=n,则有唯一解;若秩A
高斯消去法
高斯消去法gaosi xiaoqufa
解线性方程组的一种重要方法.也称之为消元法.这种方法有比较严格的程序,它分为以下两个步骤
❶顺序消元.
设方程组为
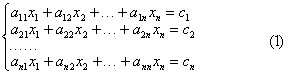
不妨假定a11≠0,先以1/a11乘以第一个方程,把x1的系数化为1,然后分别乘以-a21,-a31,…,-an1加到第2至第n个方程上,消去后n-1个方程中的x1,将方程组化为
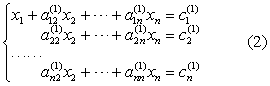
不妨设(2)中a(1)22≠0,用同样的方法把第二个方程中x2的系数化为1,并消去后n-2个方程中的x2.这样继续下去,最后得到
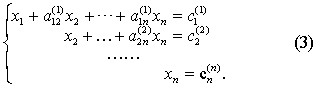
❷回代求解.
在完成第一个步骤的基础上,按相反顺序逐个消去方程组(3)中的第n-1个方程中的xn;第n-2个方程中的xn,xn-1;…;第一个方程中的xn,xn-1…,x2,得到
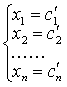
方程组
(1)中未知数的所有系数组成一个系数矩阵.

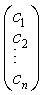
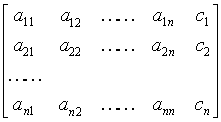

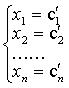
例 解方程组
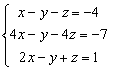
解 方程组的增广矩阵为
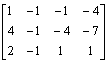
设❶,
❷,
❸分别为矩阵的第一、二、三行.现在对矩阵作初等变换.
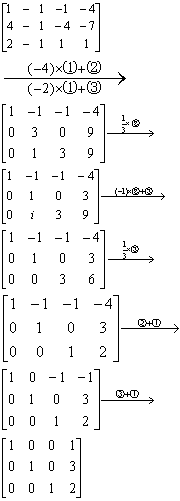
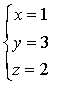
☚ n元方程 消元法 ☛
- 看守勤务是什么意思
- 看守员是什么意思
- 看守城门的人是什么意思
- 看守城门的官吏是什么意思
- 看守所是什么意思
- 看守所所官是什么意思
- 看守所所长是什么意思
- 看守政府是什么意思
- 看守费是什么意思
- 看守长是什么意思
- 看守门户是什么意思
- 看官是什么意思
- 看客是什么意思
- 看客的是什么意思
- 看家是什么意思
- 看家基因是什么意思
- 看家屋是什么意思
- 看家戏是什么意思
- 看家护食是什么意思
- 看家拳头是什么意思
- 看家拳头——留一手是什么意思
- 看家料户是什么意思
- 看家方是什么意思
- 看家望门是什么意思
- 看家本事是什么意思
- 看家本领是什么意思
- 看家狗是什么意思
- 看家的是什么意思
- 看家的本事是什么意思
- 看家道是什么意思
- 看密匝匝蚁排兵,乱纷纷蜂酿蜜,急攘攘蝇争血.是什么意思
- 看密匝匝蚁排兵,乱纷纷蜂酿蜜,急攘攘蝇争血。是什么意思
- 看富贵是什么意思
- 看对是什么意思
- 看对方脸色行事是什么意思
- 看对方脸色说话是什么意思
- 看对联是什么意思
- 看对象是什么意思
- 看小是什么意思
- 看尘世,鳌宫又报鲸波浅。是什么意思
- 看尽人间兴废事,不曾富贵不曾穷。是什么意思
- 看尽旧时书,洒尽今生泪。是什么意思
- 看尽鹅黄嫩绿,都是江南旧相识是什么意思
- 看屁股是什么意思
- 看屋是什么意思
- 看屋场是什么意思
- 看屋子是什么意思
- 看屋宇是什么意思
- 看屋梁著书是什么意思
- 看屋的是什么意思
- 看山东亭坐,待月南原行。是什么意思
- 看山吃山,看水吃水是什么意思
- 看山掠龙是什么意思
- 看山楼是什么意思
- 看山水是什么意思
- 看山爽是什么意思
- 看山看水殊未厌,栽桑栽竹粗已谙。是什么意思
- 看山笏是什么意思
- 看山色是什么意思
- 看山诗思远,对客酒杯宽。是什么意思