高斯定理gaosi dingli

关于闭合曲面电通量的定理，是静电场的基本方程之一。其内容表述如下：通过一个任意闭合曲面S的电通量Φg等于该曲面所包围的所有电荷的电量的代数和∑q除以ε0，与闭合面外的电荷无关。用公式表示为：

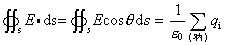
高斯定理中的闭合曲面通常叫高斯面，符号_s表示沿所要求的高斯面（一个闭合曲面）S的积分。定理内容明确指出ΦE与闭合面外的电荷无关，即不论面外有无电荷或分布如何，都不影响穿过闭合曲面的通量。ΦE只取决于闭曲面内电量的代数和。在真空的情况下，∑_qi是闭曲面内自由电荷的代数和（这时只存在自由电荷）；在介质存在时，∑_qi是闭曲面内自由电荷和极化电荷的代数和（这时面内可能存在这两类电荷）。高斯定理反映了静电场是有源场这一特性。凡是有正电荷的地方，必有电力线发出；凡是有负电荷的地方，必有电力线会聚。正电荷是电力线的源头，负电荷是电力线的尾闾。将高斯定理应用于静电平衡下的金属导体，得出其内部电场E内=0，导体内部无宏观电荷分布。电荷分布在导体外表面。这一结论在理论和实践方面都有重要意义。高斯定理是由库仑平方反比定律导出的。用这一结论人们间接验证库仑定律，借助这一结论人们制做了静电加速器等等。对于某些电荷对称分布的电场，直接由平方反比（库仑定律）关系进行计算是困难的，如均匀带电球体的电场，无限大均匀带电面的电场，以及无限长均匀带电圆柱的电场。通过对称性的论证，由高斯定理可较容易的求得这些分布的场强。例如由高斯定理求得均匀带电球壳在外部空间产生的电场，与其上电荷全部集中在球心时产生电场一样，即E=q/4πε0r2,r为球心到场点的距离，q为均匀带电球体的总电量，r>R,R为球半径。均匀带电球体内一点的场，其r

高斯定理

反映电位移与电荷分布之间普遍关系的定理。可表述为：电场中通过任意闭合曲面的电通量与该曲面所包围的自由电荷成正比。它是库仑定理与电场强度叠加原理的结果，是描述电磁现象的一个基本定理。