预期收益和标准差的计算

根据上述原理，先须计算出从市场上选出的若干证券所建成的许多不同组合的预期收益和标准差，以凭比较选择，计算各组合的预期收益比较简单，即算出包含在一个组合里各种个别证券预期收益的加权平均数，可用下列公式求得：

_p=证券组合的预期收益
X_i=证券i在组合内证券总值中所占的比重
_i=证券i的预期收益
N=组合中的证券种类数
计算一个组合的标准差，就不是这样简单，因为它并不只是个别证券的标准差的加权平均数，须用以下公式求得：

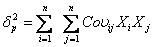
δ_P²=组合的方差
Cov_ij=证券i和证券j的收益之间的协方差。
X_iX_j=分别证券i和证券j的权数。
式中的方差(Variance)是指标准差的倍数，即δ²；相反，标准差倍数的开方值，即为，可见，二者是相通的。协方差(Covariance)表示证券收益之间的相互关系，常用统计上的相关系数(ρ)这一指标来说明，可用下式表示：

相关系数的特点，是它的数值总是在-1到+1之间。如果两种证券的收益表明是完全正相关，ρ_ij将等于+1；如果两种收益是完全负相关，ρ_ij将等于-1；如果两种收益之间毫无相关，Cov_ij和ρ_ij都等于0。
上式中的双加总符号表示所有有关证券收益的协方差都要相加，所以上列公式可用下列公式表示：

式中的前半部δ²_iX²_i，是指每种证券的方差乘上权数的平方加总；其后半部2∑Cov_ijX_iX_j，是指所有单独协方差乘以各自的权数后加总，然后乘上2。如果一个组合中含有n种证券，则所有单独协方差的数目，可由(n²—n)/2求得。
上面提到：Cov_ij=P_ijδ_iδ_j，所以上式也可改为：

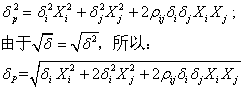
此公式就是计算一个组合的标准差的公式。
从上式中可以看出，δ²的大小，受ρ_ij的影响很大。如果ρ_ij是+1，则δ_P等于组合所构成证券的加权平均标准差，分散不会使风险减少。如果ρ_ij是-1,δ_P等于0，如果ρ_ij是0，表示两种证券收益之间没有相关，则一般来说，分散也不发生作用。所以，想要通过分散能减少风险多少，须以所计得的相关系数的大小为转移。