韦布尔方程Weibull equation

概率密度函数之一。彭尼帕克(Pennypacker,1980)将其引入植病流行学中病害季节性流行动态的研究，其微分形式为：

dX/dt=c/b(t-a/b)^(c-1)exp[-(t-a)/b]^c

积分形式可写成：

X_t＝1-exp{-(t-a)/b〕^c}

(b>0,c>0,t>a)

式中 X_t为时间t时的病情百分率；a为位置参数，决定病害始发期；b为比率参数，决定流行速度；c为流行曲线的形状参数，决定流行的先后速度的相对快慢。
由于方程有三个参数，其种种组合可描述多种形式的流行曲线，因此也称弹性模型(flexible model)。当c=1时，韦布尔方程可代替指数模型用来描述单年病害流行。当c=3.6时可代替逻辑斯蒂模型用于描述单年流行病害的流行。式中的a为病害数量开始增长的日期。因此，只有t>a时，病害才会发展。参数b决定流行速率，其取值大小与流行速率呈反相关，即b值越大，流行速率越小。

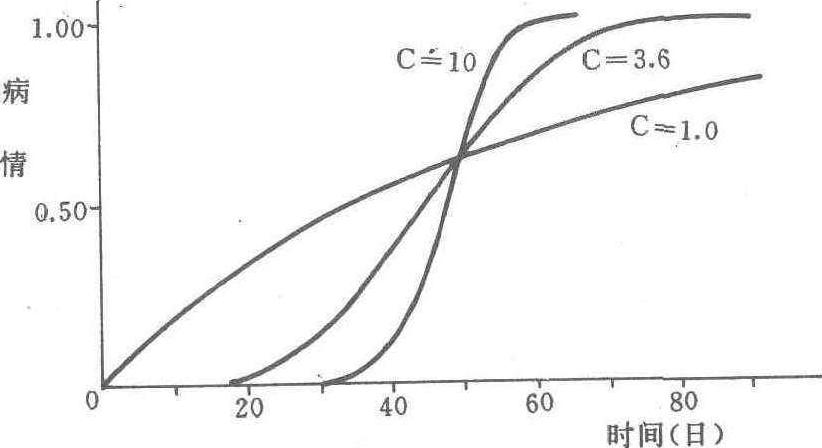
韦布尔模型的各种曲线形式
(引自曾士迈，1986)
(a=0,b=50)

韦布尔函数的特点是可以通过对参数a、b、c的调整来描述多种形式的流行曲线，如前期增长快，后期增长慢或前期增长慢，后期增长快等情况。
由于韦布尔函数没有反映初菌量的参数，在解释流行和预测病情时受到局限。