集合论jihe lun

德国数学家康托儿于19世纪末创立的，以集合为研究对象的一个数学基本分支.集合论的内容几乎渗透到数学的一切领域，它在现代数学的发展中起了很大的作用，是现代数学各个分支的基础.按照现代数学的观点，数学各个分支都可以看作是研究具有某种特定结构的集合.例如，中学数学中几何学可以看成是研究点的集合；代数学可以看成是研究数的集合以及这些集合的运算规律等.
集合论的发展可以分为两个阶段：
朴素集合论 这个阶段是从康托儿创立集合论开始到1908年.1874年康托儿摆脱了“数”的限制，首次提出具有一般化的集合概念.在集合概念的基础上，定义了集合的子集、幂集、并集、交集、直积、以及集合到集合的映射等一系列概念.后来为了解决刻画无限集合元素的多少和集合中元素间可能出现的顺序等问题，康托儿又分别引出了集合的势（集合的基数）和序数的概念(参阅“集合的基数”和“序数”).
公理集合论 1900年前后，由于集合论本身出现了悖论(参阅“罗素悖论”)，说明了朴素集合论本身的不协调，当时人们认为是敲响了这门学科的丧钟，并对数学推理的正确性产生了怀疑，而被称为数学史上的第三次危机.为了克服悖论给集合论带来的困难，当时有蔡梅罗、弗伦克尔等一些数学家致力于研究产生这些悖论的原因和解决问题的办法，因而有公理化方案的提出，产生了多种集合论公理系统.各种公理化集合论都只是朴素集合论的严格处理而已.

集合论

数理逻辑的基本分支之一。研究集合的性质及集合间的关系，特别是研究无穷集合和超穷数。逻辑和数学所研究的对象都可以认为是某些特殊的，由元素所组成的集合。这意味着逻辑和数学的各分支可以在集合论的范围内形式地定义和处理；逻辑和数学的许多基本问题可以化为集合论问题。

集合论

集合又称集，是近代数学的基础，它可以表示概念、性质、运算和变换，可以表现判断和推理，能够将数学描述表达成各门学科的语言和系统。一个集合是由一些具有某种属性的事物的全体组成的。集合论是描述人脑思维对客观事物识别和分类的数学方法。对给定的论域U与给定的性质P，造集的过程是人们对元素u∈U与性质关系的识别过程，由于识别的准则不同，因而便有了不同的集合论——普通集合论、模糊集合论、可拓集合论。普通集合论又称经典集合论、康托集合论，由康托创立。它是在以下两个条件下建立的：对识别过程规定如下准则：“只允许考虑如下两个命题：(1)元素u(∈U)具有性质P;(2)元素u(∈U)不具有性质P。而且要求对每个u∈U，这两个命题有且仅有一个成立。所有能使第一个命题成立的元素组成一类，能使第二个命题成立的元素组成另一类。经典集合论中的基本要求是：从论域U中任意指定一个元素u及任意一个集合A，要么u∈A，要么u⋶A，二者必居其一，且仅居其一。描述普通集合A一般用其特征函数XA,XA:U→{0,1},u→XA1元素u(∈U)具有性质P;(2)元素u(∈U)不具有性质P。而且要求对每个u∈U，这两个命题有且仅有一个成立。所有能使第一个命题成立的元素组成一类，能使第二个命题成立的元素组成另一类。经典集合论中的基本要求是：从论域U中任意指定一个元素u及任意一个集合A，要么u∈A，要么u⋶A，二者必居其一，且仅居其一。描述普通集合A一般用其特征函数XA,XA:U→{0,1},u→XA(u) =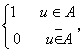
因而在经典数学中，集合运算可归结为对元素以XA(u)进行运算。普通集合论是整个经典数学的基础，是研究精确数学的强有力的工具，它是以形式逻辑为其推理准则的。
模糊集合论
模糊集合是在下列三个条件下建立的：
对识别过程规定如下准则：“只允许考虑如下三个命题：(1)元素u(∈U)具有性质P;(2)元素u(∈U)不具有性质P;(3)允许存在这样的中介元素u∈U，它使前两个命题各在一定程度上均成立。即对每一个元素u∈U，要么第一个命题成立，要么第二个命题成立，要么两个命题各在一定程度上均成立。”
模糊集合研究的是概念没有明确外延的事物，即它刻划了此事物与彼事物相互过渡过程中的中介性质。普通集合是模糊集合在退化条件下的特殊形式。模糊集合用其隶属度函数描述：定义映射μA:∪→[0,1],u→μA(u)∈[0,1]，其中A是模糊集合的表示形式，μA(u)表示了u，对模糊集合A的隶属程度。模糊集合弥补了普通集合在描述具有“亦此亦彼”特性的事物的不足，是研究模糊性事物的有力工具，它是以模糊逻辑为其推理准则的。目前，模糊集合已在自然科学与社会科学中有广泛的应用。
模糊集合是1965年由美国加利福尼亚大学控制论专家查德(L.A.Zadeh)创立的。
可拓集合论
可拓集合是在下列四个条件下建立的：
对识别过程规定如下准则：“(1 )元素u(∈U)具有性质P;(2)元素u(∈U)不具有性质P;(3)可使原来不具有性质P的元素具有性质P;(4)元素u(∈U)具有性质p，又不具有性质P。对每一个元素u∈，上述四个命题中的某一个成立。”可拓集合描述的是既非普通集合描述的“非此即彼”又非模糊集合所描述的“亦此亦彼”的特性的事物。例如，半导体，既有导电的性质，又没有导电的性质，是可拓集合描述的对象。可拓集合用其关联函数K描述：定义映射K:U→(^-∞+∞),u→K(u),K(u)称为u与可拓集合的关联度。可拓集合能够比较合理地描述自然现象和社会现象中各种事物的内部结构和彼此之间的关系以及事物的变化，它把经典集合中的逻辑值从{0,1}扩展到(-∞,+∞)，使经典数学中“属于”与“不属于”集合的定性描述拓展到定量描述，以表征元素间的层次关系。目前，可拓集合特别是在处理不相容性的决策中已取得了广泛的应用。

集合论

set theory