随机变量

设(Ω,F,P)为一概率空间，对于样本空间Ω中的任一事件ω,ξ(ω)是一个取实值的单值函数，若对于任一实数x,是一随机事件，亦即属于事件域F，则称ξ(ω)为随机变量，有时也简写ξ(ω)为ξ，直接称ξ为随机变量。常被应用于测验分数统计中。

随机变量suiji bianliang

设随机试验的样本空间为Ω，若对于每一个可能的试验结果（样本点）ω∈Ω，都唯一地存在一个实数值X (ω)与之对应，且对所有的实数a,{ω|X (ω)≤a}是随机事件，则称X (ω)为一个随机变量，简单地记作X。常用大写拉丁字母X,Y (或希腊字母ξ,η)等表示随机变量。
若X和Y是随机变量，则X+Y,X-Y,X/Y (Y,≠0)和aX+bY (其中a,b是两个常数)都是随机变量。
比如，某射手每次射击，击中目标的概率都是p(0

射击次数”x是一个随机变量，x可以取到一切自然数。
随机变量通常分为离散型随机变量和非离散型随机变量。在非离散型随机变量中，重要的且经常遇到的是连续型随机变量。

射击次数”x是一个随机变量，x可以取到一切自然数。>

随机变量Suiji bianliang

描述随机试验结果的变量。随机试验的每一个可能出现的结果都对应于随机变量的取值。如对于掷硬币这一随机试验，规定0表示出现正面，1表示出现反面，即可定义一个随机变量x，它有0和1两个取值。若随机变量的可能取值能够一一列举出来，则称之为离散型随机变量。若随机变量的可能取值是充满某一区间，则称之为连续型随机变量。随机试验中各种可能出现的结果的概率分布的情况，称为对应的随机变量的概率分布。对于离散型随机变量，每个取值对应有一个概率值；对于连续型随机变量，谈论每个取值的概率的绝对大小无意义，只可确定各取值的概率的相对大小，或是某一区间内取值的概率大小。

随机变量

概率论的一个基本概念。表示随机现象结果的变量，随出现结果数量的不同取不同的数值。例如电讯局每小时的话务量就是一个随机变量。

随机变量Random Variable

根据概率不同而取不同数值的变量，叫随机变量。一个随机变量具备以下特征：它可以取到许多不同的值，每个值都可以被一个小于或等于1的概率取到，所有这些概率和为1。按随机变量取值情况可以把随机变量分为两类：离散性随机变量(discrote randorn variable)和连续型随机变量(continuous random variable)。如果随机变量只能取有限个或可列个可能值，而且会以确定的概率取到这些值，则称它为离散型随机变量。一般用概率函数或分布表来表示离散型随机变量的分布。对于任何实数x，如果随机变量的分布函数F(x)可以写成：

其中(x)≥0，则称ζ为连续型随机变量。(x)为ζ的概率分布密度函数。
n元随机变量定义如下：如果每次试验的结果对应着一组确定的实数(ζ₁，…，ζ_n)，它们是随试验结果不同而变化的几个随机变量。如果对组实体x₁，…，x_n事件“ζ₁⊂x₁，…，ζ_nn”有着确定的概率，则称n个随意变量的总类ζ₁，…，ζ_n为一个n元随机变量。类似的有，如果二元随机变量(ζ,η)所有可能的取值为有限个或可列个，并且以确定的概率取不同数值，则称(ζ,η)为二元离散型随机变量。n元离散型随机变量以此类推。如果存在一个非负函数(x,y)，使得二元随机变量(ζ,η)的分布函数F(x,y)，对于任意实数x、y都有：

则称(ζ,η)是二元连续型随机变量。(x,y)称为ζ与η的联合分布密度函数。n元连续型随机变量以此类推。

随机变量Random Variable

表示随机现象各种结果的变量。随机变量取值有限的称为离散型随机变量，取值不可列的称为连续型随机变量。随机变量与一般变量的主要差别表现在：
❶取值的随机性，即随机变量取哪个值事先不能确定；
❷取值的统计规律性，即随机变量取某个值或在某一区间内取值的概率是完全确定的。例如，单位时间内电话总机收到的呼唤次数、测量的误差等都是随机变量。

随机变量

反映随机事件的变量。对于某种经济活动或经济现象来说，一方面，其未来的变化和结果有其自身的规律和相应的因果关系；但另一方面，由于其发展变化不是孤立的，要受到各种人为的或其他变化着的因素的影响，因而其未来的变化和结果有可能发生，也有可能不发生，即具有一定的确定性和一定的不确定性。具有这种特点的经济活动或经济现象称为“随机事件”。衡量随机事件出现的可能性大小的量称为“概率”。在一个描述经济变量之间关系的数学方程式中，加进一个反映随机因素的扰动项(或称“误差项”)，可以使其更符合客观实际。比如，在研究某一经济现象时，影响其变化的因素很多，不可能将所有因素都包括进模型中，而只能包括其中的一个或几个主要因素，其他一些因素则被省略掉。这些被省略的因素的影响，就可以反映在随机扰动项之中。这种带有随机扰动项的数学模型，称为“随机模型”。

随机变量

随着抽样结果的情况不同，而取不同值的变理，称随机变量。通常的随机变量可分作离散型随机变量和连续型随机变量两类。如果随机变量X的值可一一列举，则称为离散型随机变量； 如果X的取值可以充满某一区间，就称为连续型随机变量。比如，投保人的年龄，就可以用一个实变数X来表示，每个投保人都有个年龄数相对应，而且，当随机地抽出一个投保人时，其年龄是事先不能确定的，因此年龄就作为一随机变量。

随机变量random variable

在随机检验中被测量的变量。在日常生活中我们遇到许许多多的不确定性的现象，比如投掷硬币时是出现正面还是反面；在企业产品检验过程中出现废品数等。对于这些事件的测度就称为随机变量。其严格的数学定义是：
设ξ(ω)是定义在概率空间(Ω,ζ,P)上的单值实函数，如果对于直线上的任一波雷尔点集B，有
{ω:ξ(ω)∈B}∈ζ
则称ξ(ω)为随机变量。而P{ξ(ω)∈B}称为随机变量的ξ(ω)概率分布。以上符号中Ω,ζ和P分别表示样本空间、事件域和概率。
随机变量实际上是样本空间中任何点取得实值的可测函数。它可以分为离散型和连续型两种。前者指随机变量的取值为有限个或者至多可列个，比如废品个数、一定时间里电话的呼叫次数等，其可能结果都可一一列举出来。后一种指随机变量的取值为不可列个，它可在某个区间[a,b]或者(-∞,∞)取值，比如风速、降水量等等。

随机变量

随机事件有各种不同的结果，变量X按不同结果而取不同的值，且X服从一定的概率分布，这样的变量称为随机变量，它是随机事件的数量化。随机变量的分布型常用的有离散型与连续型两种，均可用分布函数表达随机变量的概率性质。但在许多实际问题中，有时很难精确地求出其分布函数，或只需要知道某一、二个描述分布特征的数字指标（称数字特征）就够了。常用的数字特征有数学期望、方差、矩等。
离散型分布 如果随机变量X只能取有限个数值X₁,X₂，…，X_n；或无限可数个数值X₁,X₂，…，X_n，…，就说X为离散型随机变量。当X=X_k (其中k=1,2，…)时的概率记作p(X_k),∑p(X_k)=1。p(X)称为概率函数。则X的取值及其对应的概率可按一定次序一一列举，例如以某种动物作某药的毒性试验时，已知其死亡率为60%。则4个动物作该药的毒性试验时死亡X只及其对应的概率为

动物死亡数X	0	1	2	3	4
对应的概率p(Xk)	0.0256	0.1536	0.3456	0.3456	0.1296

当随机变量取值不大于X时的累计概率记作P(X)=

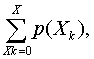
称为离散型分布函数，如本例，动物死亡数
不大于2只的累计概率为
P(2)=p(0)+p(1)+p(2)
　=0.0256+0.1536+0.3456=0.5248。
二项分布、Poisson分布、超几何分布等都是离散型分布。一般说来，离散型分布多用于计数资料。
连续型分布 例如成年男子的身高，人的寿命等不是离散型随机变量。对非离散型随机变量，由于其可能取的值不能一个一个地列举出来，因而转为研究随机变量的取值不超过X (注： 本分卷中X既表示随机变量也表示它所取的值)的概率，称为分布函数，记作F(X)。如果随机变量X的分布函数F(X)能够表示为

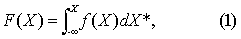
就说X为连续型随机变量，式中非负函数f(X)称为此分布函数(或分布，或随机变量)的密度函数，简称密度。例如某市120名12岁男孩身高(cm)的频率分布服从正态分布，其均数为143.1cm，标准差为5.67cm，则它的密度为

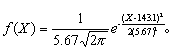
该市12岁男孩身高不超过143.1+5.67=148.77cm的概率为

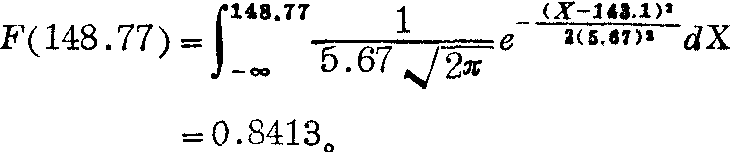
严格地说，式(1) 应表示为
对于某些常见分布，已知X求F(X)值有统计表可查，如上例可由标准正态分布曲线下的面积表查得(见条目“正态分布”)。正态分布、x²分布、Weibull分布等都是连续型分布。一般说来，连续型分布多用于计量资料。
数学期望 设有一个含量为n的样本，观察值X₁ ,X₂，…，X_k的权数依次为，f₁,f₂，…，f_k，则其均数为

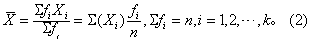
当n充分大时，频率fi/n接近于概率。从这个加权均数的启发，我们定义离散型随机变量X的数学期望E(X)为
E(X)=∑X_p(X)。(3)式中∑p(x)=1，并要求E(X)为一确定的数值。由此可见，数学期望就是总体均数，常简记为μ。
类似地，对具有密度函数f(X)的连续型随机变量，有

这里同样要求E(X)为一确定的数值。
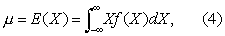
方差 数学期望刻划了随机变量的集中位置，进而刻划它的变异程度的有方差。对于离散型随机变量X的方差定义为
V(X)=E[X-E(X)]²＝∑(X-μ)²p(X); (5)对于连续型的，定义为

式(5)与(6)中都要求V(X)是一个确定的数值。
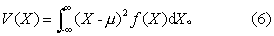
有了数学期望（总体均数）与方差的定义就可按上列公式，计算随机变量的数字特征。例如当X服从二项分布时，可按式(3)、(5)，求得它的数学期望为nπ，方差为nx(1-x); 当X服从正态分布时，可按式(4)、(6)求得E(X)=μ,V(X)=σ²。本分卷中以σ²表示服从任何分布的随机变量的方差，即σ²＝V(X)。
矩（动差） 随机变量X的k阶中心距，记作μk，对离散型定义为
μ_k＝∑(X-μ)^kp(X); (7)
对连续型定义为

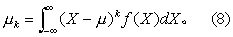
当μ=0时，k阶中心矩就称为k阶原点矩，记作μ′k，对离散型与连续型分别为

这里要求μk和μ′k都是确定的数值。当k=1时，μ′1就是X的数学期望。当k=2时，μ₂就是X的方差。三阶矩可刻划分布的偏度，四阶矩可刻划分布的峰度。

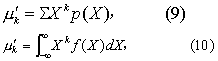
随机变量

如果影响变量值变动的因素很多，且作用的方向、程度都带有一定的波动性和随机性，这些众多因素致使变量值的大小、方向具有偶然性，这种变量称为随机变量。

随机变量random variable

具有一定概率的变量。在该变量定义域内全部相应概率之和为1。设Ω为概率空间，如果对于Ω中点ω有一个实数X(ω)和它相对应，从而得到一个定义在Ω上的实函数X(ω)，即称X为随机变量。X只取有限个或可数个不同可能值的，称为离散随机变量；如果可用一非负函数f(X)的积分表示X在一定区间上的概率的，则为连续随机变量。

随机变量random variable

描述随机现象各种不同结果的变量。随机现象的每一种结果称一个随机事件，它在一次具体实践中可能发生，也可能不发生，经过大量观察，它们发生的可能性具有一定的规律性。随机变量的每一个值表示一个具体的随机事件。心理与教育研究中很多变量都没有固定取值，在理论建构时，经常把其当作随机变量，如反应时、态度水平、工作效率等。

随机变量

概率论的基本概念。描述随机现象各种不同结果的变量。随机现象是指具有以下三种特性的现象。(1) 现象有多种不同的结果，所有可能结果是已知的；(2) 现象出现何种结果在发生之前无法预料；(3) 在相同的条件下现象可以重复发生。随机现象的每一种结果称一个随机事件，它在一次具体实践中可能发生，也可能不发生，经过大量观察，它们发生的可能性具有一定的规律性。随机变量的每一个值就是表示一个具体的随机事件。