刚体的定点运动

---

2．6．1 欧拉角和运动方程

刚体运动时，其上或与其固连的空间内存在一个始终不动的点，则刚体的运动称为定点运动。确定定点运动刚体的瞬时位置需要三个独立参数。由欧拉首先提出的三个独立参数称为欧拉角。即以定点O为原点建立定坐标系Oxyz，以及与刚体固连的坐标系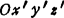′，如图1．2－13．其中平面Oxy和Ox′y′的交线为ON，称为节线。欧拉角是指下列的三个角：1．进动角ψ(为ON与OX的夹角)；2．章动角θ(为平面Ox′y′与Oxy的夹角，即Oz与Oz′的夹角)；3．自转角φ(为Ox′与ON的夹角)。显然，一组欧拉角的值(ψ，θ，φ)唯一地确定了刚体在空间的一个位置；欧拉角随时间t的变化规律，唯一地描述了刚体的运动规律。因此，欧拉角以时间t为自变量的单值连续函数，

2．6．2 刚体定点运动的分解

根据欧拉角的定义，刚体定点运动可分解为以下三种定轴转动：

❶  动坐标系Ox1y1z1相对于定坐标系Οxyz，绕轴Οz作定轴转动，其转动方程称为进动方程，即

ψ=Ψ(t)

❷ 动坐标系Ox₂y₂z₂相对于动系Οx₁y₁z₁，绕轴Ox₁作定轴转动，其转动方程称为章动方程，即

θ=θ(t)

❸ 刚体(或Οx′y′z′)相对于动系Οx₂y₂z₂，绕轴Οz2作定轴转动，其转动方程称为自转方程，即

φ=φ(t)

因此，刚体的定点运动可以视为以上三种转动的合成。反之，以上三种转动又可以视为刚体定点运动之分解。即