负二项分布negative binomial distribution

属非随机分布的一种空间分布型。抽样所得各随机变量的理论频次分布为概率论中负二项式的展开各项。种群个体分布为明显的聚集状，个体在各取样单位中出现的机会不相等。方差S2显著大于均数,S²/通常在1.5～3之间。特别是方差偏大，为泊松分布的特例，是由多个密度不同(即不同值)，而个体间呈泊松分布的集团混合而成的分布。符合奈曼分布的资料往往同时符合负二项分布，但反之却不一定符合奈曼分布，故本分布是广泛地符合于不均匀分布现象。其理论频次通式为：

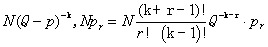
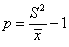式中P_r为取样单位中有r个个体的概率；，即奈曼分布的m₂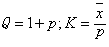；，即奈曼分布的m₁（表示个体间聚集程度）。

负二项分布

负二项分布是一种离散型的分布，可用于寄生虫学、医学昆虫学、微生物学以及流行病学等的研究。
概率函数及其图形 类似二项分布，服从负二项分布的随机变量的概率依次为负二项式展开后的各项：

负二项分布的概率函数为

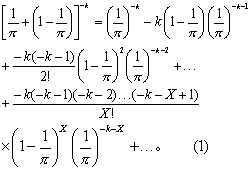
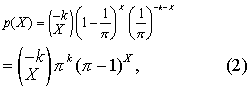
式中K>0,0<π<1,X=0,1,2，…，

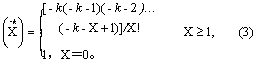
当k为正整数时，负二项分布称为Pascal分布； 当

称为几何分布。
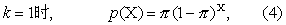
已知参数k与π，按式(2)与(3)即可算得X=0,1,2…时的各个概率，并画出负二项分布的图形。
性质
(1) 负二项分布的均数μ与方差σ2为μ=k(1-π)/π,(5)

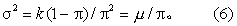
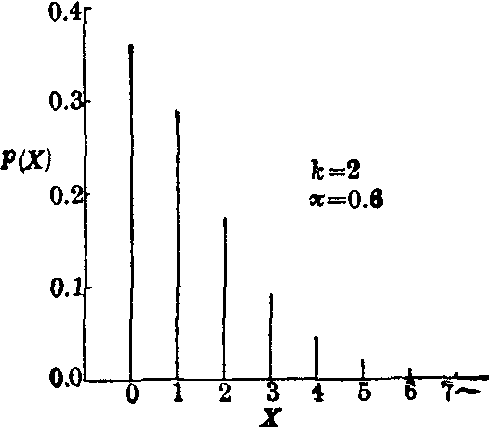
负二项分布
(2)递推公式： 当按式(2)求得p(X-1)后，即可按式(7)求得p(X),

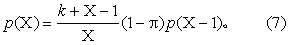
参数π与k的估计 介绍两种方法：
(1)矩法。先由样本求得均数X与方差s2，作为μ与σ2的估计值，代入式(6)算得π的估计值，再代入式(5)算得k的估计值。
(2) 频数法。此法在样本含量充分大时可得到较满意的结果，其优点是简捷易算。方法步骤是：
❶由样本求得均数作为μ的估计值；
❷由式(7)，令X=1，得

上式左端的分子分母同乘以样本含量n，得np(1)/np(0)，即X=1与X=0时的理论频数之比。当n充分大时，可以实际频数之比估计，于是此比值近似于k(1-π)。
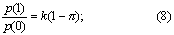
❸按式(5)及式(8)求π及k的估计值。
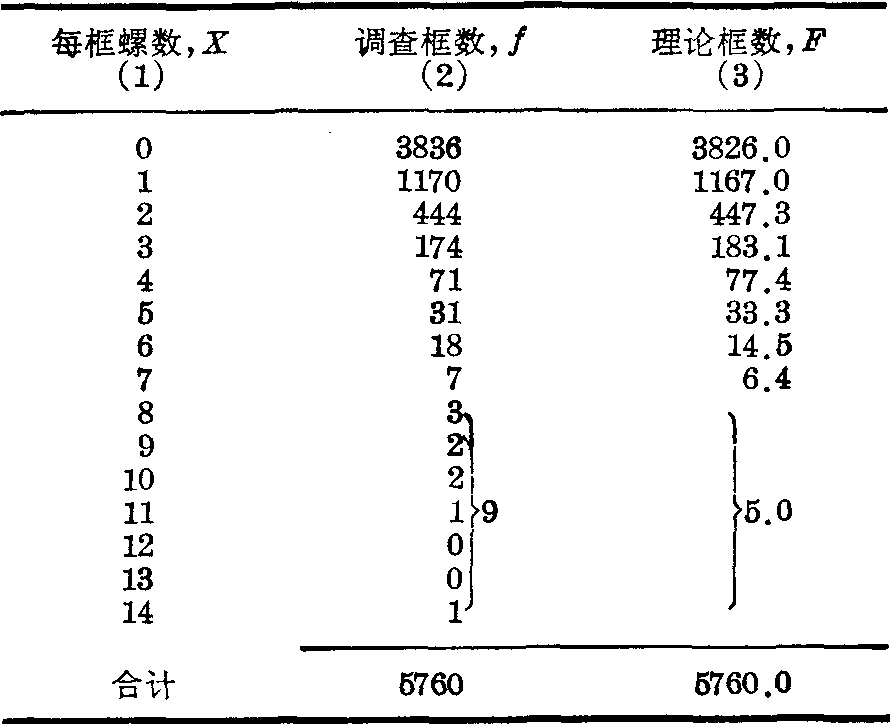
例 为了研究钉螺的分布规律，对某河岸共查螺5760框(每框1/16平方市尺)，各框内钉螺数的分布如表第(1)、(2)栏，问钉螺的频数分布是否服从负二项分布？钉螺的频数分布

H₀: 钉螺的频数分布服从负二项分布，
H₁: 钉螺的频数分布不服从负二项分布。
α=0.2。
(1)求π与k的估计值。本例n=5760，可用频数法估计之。由表算得＝0.566493，按式(8)，得

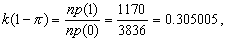
按式(5)，得

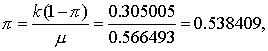
再按式(8)，得

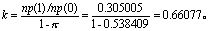
(2)求理论频数F。先求p(X)

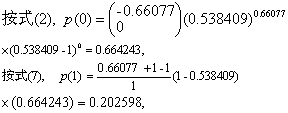
p(2)～p(7)仿此递推。
以上为理论频率，各乘以总框数5760，得上表第(3)栏F。X由0到7，累计F已达5755，故X≥8的累计F为5760-5755=5.0。
(3) x²检验。

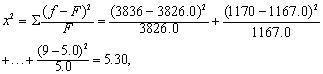
自由度v=9-3=6。
查x²界值表，P≐0.5，按α=0.2水准不拒绝H₀，故可认为钉螺的分布服从负二项分布。