角的度量jiaode duliang

由于采用的度量单位不同，常用的有以下四种度量制.
❶角度制 规定一个圆周的1/360的弧叫做一度弧.一度弧所对的圆心角叫做一度角.一度角记作1°.1°的1/60叫做一分，记作1′.1′的1/60叫做一秒，记作1″.由上述规定可以知道：1°=60′,1′=60″.用度作量角单位的制度叫做角度制，也叫做六十进制.

❷弧度制 以在圆上与半径等长的弧所对的圆心角为单位，它叫做弪，也叫做一弧度角，按照这一规定，1周角等于2π弧度，即360°=2π弧度.因此，角度与弧度有关系

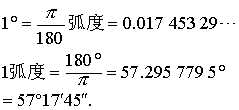
在书写中弧度的符号通常省去不写.
用弧度作量角单位的制度叫做弧度制，又叫做弪制.

❸百分制 取直角的百分之一作单位，叫做.1分为100分，1分又分为100秒.用作量角单位的制度叫做百分制.此制度是法国创立米突制时(1795年)提议的，但未得到推行.

❹密位制 把圆周分成6000等份，每一份叫做1密位的弧，1密位的弧所对的圆心角叫做1密位的角.以密位作量角单位的制度叫做密位制.密位制常在军事上应用.

---

角的度量jiao de duliang

度量角的大小的办法.度量角的单位制常用的有两种：“角度制”和“弧度制”.
角度制 把一个周角分成360等份，每一份叫做1度角，记作1°；把1度角分成60等份，每一份叫做1分，记作1′；把1分角分成60等份，每一份叫做1秒，记作1″.

1°=60′,1′=60″.

弧度制 长度等于半径的弧所对的圆心角叫做1弧度的角.
两种度量单位的换算关系如下

π弧度=180°

1弧度=180°/π≈57°17′44.8″

1°=π/180弧度≈0.017 453弧度.

在军事测量上还有一种密位制，把周角分成6000等份，每一份叫做1密位的角.

角的度量Jiao de duliang

度量角的大小的办法。度量角的单位制常用的有两种：“角度制”和“弧度制”。
❶角度制：把一个周角平均分成360份，每一份是1度，记作1°。把1度的角平均分成60份， 每一份是1分，记作1′。把1分平均分成60份，每一份是1秒，记作1″。1°=60′,1′=60″。例如，∠A=48度56分37秒， 记作∠A=48°56′37″, 读作48度56分37秒。

❷弧度制： 当圆周上某段圆弧的弧长等于这个圆的半径时，这段圆弧所对的圆心角是1弧度。用这样的单位来度量角的大小叫做弧度制。设圆的半径为r，圆周长为2πr，弧度和角度的换算关系为： 1弧度=180°/π≈57°17′45″, 1°=π/180弧度≈0.01745弧度。
度量一个角的大小时经常要用到一种仪器， 叫做量角器，也叫做半圆仪。它的形状多数是半圆形的。它是把半圆平均分成180份， 每一份所对的角叫做1度的角。量角器的刻度由两个半圈组成，按逆时针方向，内圈刻度由0°到180°, 外圈刻度由180°到0°。用量角器量角的时候，把量角器放在角的一边上面，使量角器的圆心和角的顶点重合，零度刻度线和角的一边重合，角的另外一边所对的量角器上的刻度， 就是这个角的度数。

---

角的度量Jiao de duliang

角的概念的起源无疑是很早的，但关于它的早期情况目前并不清楚。古代巴比伦人把圆周等分为360份，这无疑成了后来60进制的角度制的源头。但是巴比伦人是在他们的天文学中这样做的，并未在数学上给以研究，而且实际上他们所涉及的仅仅是弧，而不是角。另一方面，埃及人通过“进程”与 “升高”的比值研究了金字塔的陡度， 在大约公元前1650年左右的阿默斯纸草书中就有一些这样的问题， 其中确实包含了对角的概念的认识。
人们确信，古希腊第一位著名的哲学家、科学家泰勒斯(约公元前625—前547，参见该条) 已经对下列命题作了某种逻辑推理：两条直线相交，对顶角相等；等腰三角形的两底角相等；两个三角形，有两个角和一条边对应相等， 则全等。因此，至迟在公元前6世纪，希腊人已经开始对有关角的概念和命题作了数学上的理论研究。公元前5世纪，他们开始研究著名的三等分角问题。约公元前300年，欧几里得在《几何原本》一开头给出的5条公设和5条公理中， 第4条公设是：“所有直角彼此相等”， 说明角度概念在他的几何体系中占有重要地位， 有关平行线及相似形的理论就是以角的概念为基础的。
公元前 2 世纪， 希腊天文学家希帕恰斯(Hipparchus)采用巴比伦人的方法，把圆周360等分，把直径120等分，每一份再分为60小份，每一小份再分为更小的份，以此类推，这就是后世角度制中度、分、秒概念的起源。他还编制了0°—180°之间间隔为1°的弦表(后来印度人把希腊人所用的全弦改为半弦，便形成了我们所说的正弦表)。公元2世纪，托勒密以希帕恰斯、梅内劳斯 (Menelaus, 1世纪)的工作为基础，系统地整理了古希腊的三角学成果， 并且引入了今天所用的角度制中表示度、分、秒的记号°、′、″。
角的度量的弧度制 （弪制） 出现很晚， 它是1748年由欧拉正式引入的。
在中国古代的《考工记》(成书于公元前7世纪以前，一说成书于公元前4世纪)中，曾有角的概念与度量的萌芽，在这本书的“车人”章中有：“车人之事，半矩谓之宣，一宣有半谓之欘，一欘有半谓之柯，一柯有半谓之磬折。” 由于矩是直角曲尺 (参见 “尺规与规矩”), 半矩即45°, 于是：
1宣=半矩=45°,
但是，同一书中的“磬人”章中又有： “磬氏为磬，倨句一矩有半。”其中，倨指钝角，句即勾，指锐角，倨句即指角的大小，根据这里给出的关系，磬的夹角（即前面所说的磬折）为11/2矩，即135°，这与“车人”中的规定并不一致，因此，当时的角的度量还不统一，后来角的概念与度量在中国古代数学中也没有发展起来。