罗吉斯蒂人口Logistic Population

亦称“罗吉斯蒂曲线”(Logistic curve)。描述人口增长规律的一种理论。这种理论认为：人口增长最初以加速度增长，达到某一点(图中曲线上的拐点B)以后增长速度开始递减，最终达到一个为特定空间和文化阶段所规定的人口的极限L。罗吉斯蒂曲线形状如图：

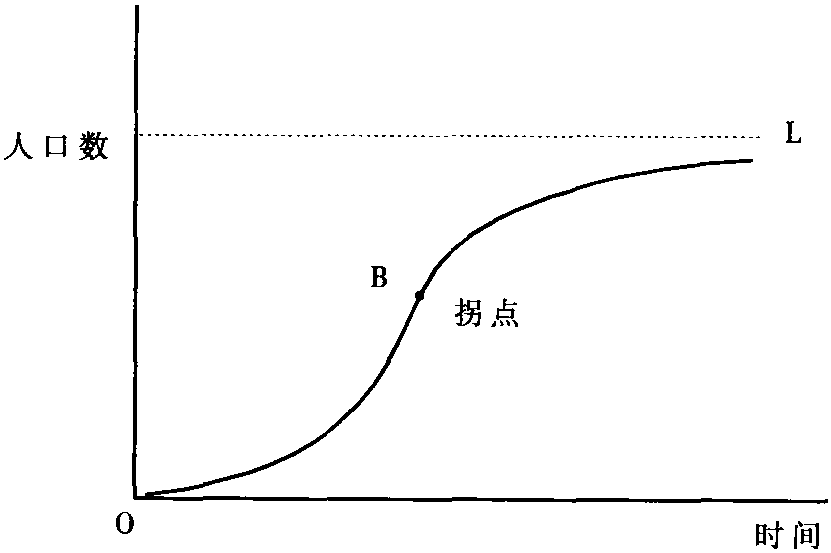
罗吉斯蒂人口方程式为P=L/1+e^a+bt，其中P为t时点的人口数，L为人口极限量（最大人口量）,e为自然对数底，a和b为有关参数。
此方程由比利时学者维尔乌斯特(P.F.Verhulst)于1938年首次提出，称之为“罗吉斯蒂曲线”。但此后这条曲线一直没有得到重视，很少有人注意它。1920年，柏尔(R.Pearl)和里德(L.J.Reed)在研究果蝇的繁殖中发现了与维尔乌斯特相同的曲线，并把它应用到人口估计和人口预测中，引起广泛注意，被视为“罗吉斯蒂曲线的再发现”。柏尔把人口增长看作时间的函数，并提出了5个条件：
❶空间有限；
❷在一定条件下人口增长有最大限度；
❸人口增长的最小限度为零；
❹人口增长带有文化阶段性或循环性，它是一个积累过程；
❺人口增长的一般形态，最初是加速增长，达到某一点（也是人口增长速度的最大点）以后，增长速度递减，最终达到一个为特定空间和文化阶段所规定的人口极限。柏尔和里德认为罗吉斯蒂曲线是人口发展规律的“通用模式”，认为一切人口数量都按这一曲线发展。