等价命题
等价命题dengjia mingti
若命题A,B保持同真或同假,则称命题A等价于命题B,记作A≡B.它是命题间的一种重要的关系,称为等价关系.具有等价关系的命题在推理中可以互相代换(代换原则).“A≡B”与“(A↔B)恒为真”是一致的.因此,命题A,B是否等价的问题,可由等值命题A↔B是否恒为真来判断.后者可通过作出等值命题A↔B的真值表直接得知.
如果把蕴涵命题“若A则B”(A↔B)称为原命题,那么由它可以作出以下几种形式的命题:“若B则A”(B→A)叫做原命题的逆命题;“若A则B(A→B)叫做原命题的否命题;“若B则A(B→A)叫做原命题的逆否命题.上述四种命题形式及其关系可用下图表示:
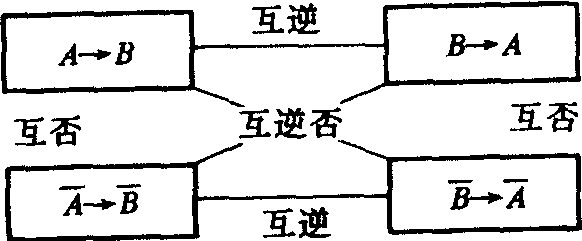
由以下真值表得知,互为逆否的命题是等价的,互为逆命题和互为否命题是未必等价的.
| A | B | A→B | B→A | Ᾱ→ |  →Ᾱ →Ᾱ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
数学中所讨论的蕴涵命题A→B,其中条件A(前件)和结论B(后件)都是具有实质联系和关系的(即实质蕴涵命题).如果A,B没有任何联系和关系,在数学中被认为是无意义的.
☚ 复合命题的构成方法 演绎推理 ☛
- 灯诱围网捕捞是什么意思
- 灯诱围网渔船是什么意思
- 灯诱渔船是什么意思
- 灯谜是什么意思
- 灯谜大全是什么意思
- 灯谜诗·天上人间两渺茫是什么意思
- 灯谜诗·镂檀锲梓一层层是什么意思
- 灯谜诗·騄駬何劳缚紫绳是什么意思
- 灯质是什么意思
- 灯镜传影是什么意思
- 灯青人已眠,饥鼠稍出穴。掀翻盘盂响,惊聒梦寐辍。是什么意思
- 灰是什么意思
- 灰是什么意思
- 灰伯劳是什么意思
- 灰分是什么意思
- 灰分元素是什么意思
- 灰分的测定计算是什么意思
- 灰分的测定计算是什么意思
- 灰包菇是什么意思
- 灰包菇是什么意思
- 灰化作用是什么意思
- 灰化土是什么意思
- 灰化层是什么意思
- 灰化法的测定计算是什么意思
- 灰化淀积层是什么意思
- 灰口铸铁是什么意思
- 灰(口)铸铁是什么意思
- 灰叶是什么意思
- 灰叶是什么意思
- 灰叶是什么意思
- 灰叶根是什么意思
- 灰叶根是什么意思
- 灰喜鹊是什么意思
- 灰喜鹊(Cyanopica cyana swinhoei)是什么意思
- 灰头麦鸡是什么意思
- 灰姑娘是什么意思
- 灰姑娘是什么意思
- 灰姑娘型故事是什么意思
- 灰子南瓜是什么意思
- 灰尘是什么意思
- 灰尘自然沉降量的测定计算是什么意思
- 灰巴蜗牛是什么意思
- 灰市是什么意思
- 灰市和灰市价格是什么意思
- 灰市场理论是什么意思
- 灰弹散是什么意思
- 灰心是什么意思
- 灰心丧气是什么意思
- 灰心丧气是什么意思
- 灰心丧气是什么意思
- 灰心丧气是什么意思
- 灰心丧气是什么意思
- 灰心丧气是什么意思
- 灰心丧气 兴高采烈是什么意思
- 灰心丧气效应是什么意思
- 灰心槁形是什么意思
- 灰数学引论——灰色朦胧集是什么意思
- 灰(斑)鸻是什么意思
- 灰日暴动是什么意思
- 灰暗区域措施是什么意思