第一宇宙速度diyi yuzhou sudu

人造卫星绕地球运动的圆形轨道半径等于地球半径时卫星所具有的速度。又称环绕速度。牛顿曾经计算水平抛出的石头永不落回地面的速度约8千米/秒。现代公认的第一宇宙速度值约等于7.9×10³米/秒，这个数值可以由牛顿运动定律和万有引力定律计算得出。设质量为m的卫星在离地面h高处作匀速圆周运动，它所需的向心力应等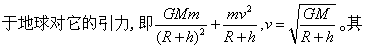中M为地球质量，R为地球半径，G为万有引力常数，v为卫星的速度。可以看出h越大，即卫星离地面越高，它环绕地球运动的速度越小。当轨道半径等于地球半径时(h=0)，将G=6.67×10-¹¹牛·米²/千克²,M=5.98×10²⁴千克，R=6.37×10⁶米代入上式，可以求出第一宇宙速度的数值v=7.91×10³米/秒≈7.9×10³米/秒。在地球表面附近，如果抛射体的水平速度小于第一宇宙速度，它就不能成为卫星，抛体运动的轨迹将是椭圆(h较小时可近似为抛物线)的一部分。所以第一宇宙速度也是在地面附近使卫星进入圆轨道所必需的水平速度。由于运载卫星的火箭在离开地面向上飞行时，要穿过地球周围稠密的大气层，如果飞行速度很大，一方面由于低空大气的阻力与飞行速度的三次方成正比，会耗费大量的能量；另一方面因空气摩擦而产生的高温可能给火箭和卫星带来灾难性的后果，所以实际发射时，总是以较低的飞行速度穿过稠密大气层，在大气层以外的高空中实现加速。第一宇宙速度要用多级火箭发射卫星才能达到。

第一宇宙速度

见“宇宙速度”。