种群增长型population growth form

种群数量增长的特征和方式。当种群占据新的适宜的环境或渡过不良气候后遇到适宜条件时，通过繁殖增加个体数量。不同种群由于其繁殖特性的差别，表现出不同的增长特征。种群增长可分为J形增长型和S形增长型。在此基础上，又因不同的生物和环境特点，表现出各种综合的或过渡的类型。
J形增长型 种群在无限环境条件下，以几何级数（等比级数）增长，又称指数增长，是种群增长的最简形式。最初由海尔(S.M. Hale) 1677年提出，后为马尔萨斯(T.R. Malthus) 1798年重新发现，因而又称海尔-马尔萨斯增长。根据世代是否重叠将指数增长分为两类： ❶离散增长。世代不重叠，亲代和子代不能同时繁殖，种群增长是不连续的。如某种群在一个繁殖季节t₀时有10个雌体 (No=10) 和同等量的雄体，用雌体产雌体表示种群增长。到下一个繁殖季节t1时，种群数量为200个雌体(N1=200)，经过一个世代，增长率λ=N1/N0=20，假定种群年复一年地以上述比率持续增长，可用下式描述：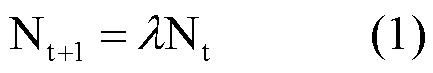
或 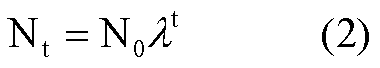(2)λ是世代不重叠种群等比级数增长的公比，称周限增长率。
❷连续增长。世代重叠，子代和亲代可以同时繁殖，种群增长是连续的，用微分方程描述：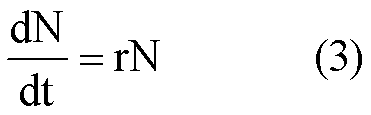

其积分式为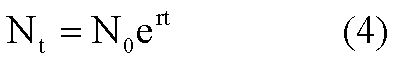： r是种群的瞬时增长率，e是自然对数的底。
S形增长型 种群在有限环境条件下随着密度的上升，对有限资源和其他生活必须条件的种内竞争也随之加剧，使种群增长率下降。假定这种影响随着种群密度的上升按比例地增加，并且当种群密度达到环境容纳量时，种群停止增长，则种群增长曲线表现为S形。S形增长又称逻辑斯谛增长，最初由维尔富斯特(P. F. Verhulst) 1838年提出，后为皮埃尔(R.Pearl)1920年重新发现，故又称维尔富斯特—皮埃尔增长。描述S形增长的数学模型为下列微分方程：

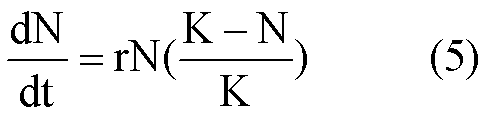
式中 K是S形曲线的上渐近线，代表种群所能达到的最大值，称为环境容纳量，亦称饱和密度；a是初始密度No所决定的一个常数。(5)式是在(3)式中引入限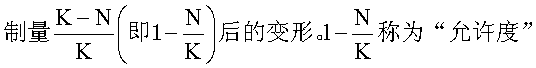即未实现的增长占环境容纳量的比率，它是种群瞬时增长率实现程度的修正值，其数域在0～1之间。当N很小时，允许度近似最大值1，种群增长迅速，与J形增长极相似； 随着N值的增长，允许度逐渐变小，r的实现程度按比例下降，两条曲线逐渐分开； 当N值达到K/2时，种群增长率dN/dt达到最大值； 当N值接近K时，dN/dt接近零。N=K/2是曲线的拐点，在此之前dN/dt随种群增加而上升，称正加速期，此后为负加速期。逻辑斯谛增长揭示了种群内部存在的一种对增殖起抑制作用的负反馈机制。属于J形增长的种群，密度增加迅速，很快达到环境容纳量，然后突然停止增长，这表明环境阻力或其他限制因子是突然产生有效影响，所以J形增长型可以看作是S-形增长型的一个特殊形式（见图）。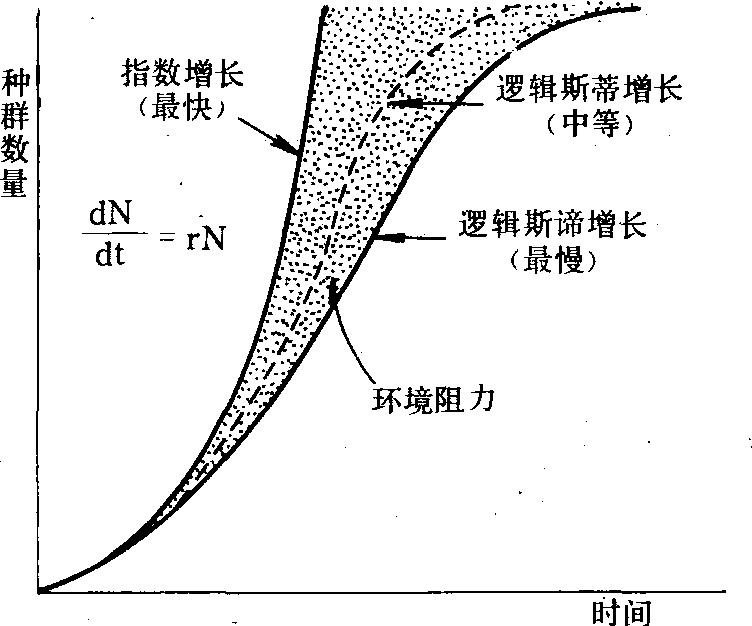

种 群 增 长 型

自然情况下，严格地符合上述模型增长的种群虽不多，但模型为解释自然界中千差万别的种群增长形式提供了方法，有助于揭示种群增长的内部机制，参数r、K有其明确的生物学含义，它们在分析种群动态及进化选择中有着重要意义。
实验室中可以培养出符合模型增长的种群。在自然界，某些细菌、昆虫、鼠类的繁殖，一年生植物干物质重量的增加，在有利季节里，短时期内呈J形增长，多数生物的增殖，包括植物分蘖的增加，株高的增长，在某时期内，表现出S形增长。种群的逻辑斯谛增长模型是生物资源开发中最大持续产量理论的重要依据。

种群增长型pattern of population growth

表征种群数量变化动态的模型。种群在适宜的环境条件下通过繁殖增加个体数量，其数量变化动态受环境条件的制约，与增殖、衰亡和迁移有关。种群数量增长有两种基本类型，即J型增长和S型增长。前者是种群在无限环境条件下的数量变化动态模型，后者是种群在有限环境条件下的数量变化动态模型。若环境资源不受限制，种群增长率恒定，则该种群的个体数量呈指数形式增长，增长曲线呈J形，故称J型增长，又称指数增长。但是在自然界中，环境资源有限，种群数量增长随着环境阻力增大、种内竞争加剧而变慢，由于环境对种群增长的限制是逐渐增加的，越接近环境所能支持的最大负载量，种群的数量越趋于稳定，其增长曲线呈S形，故称S型增长，也称逻辑斯谛增长。自然界种群数量动态是极其复杂的，J型增长和S型增长只是其中两类代表类型。