相关系数

用来度量两个随机变量间线性关系大小程度的一个量，用ρ表示。如果用X与Y表示两个随机变量，σ(X)与σ(Y)分别表示它们的标准差，用cov(X,Y)表示它们的协方差，则ρ=。当有了两个随机变量的一组样本观察向量(x_i,y_i),i=1,2，…，n后，它的估计用r（也称为样本相关系数）表示，则r=(x_i-x-)(y_i-y-)(x_i-x-)²(y_i-y-)²。常被应用于测验分数统计中。

相关系数coefficient of correlation

统计学上指两组变数x和y的坐标点呈直线型时，表示两变数间相互关联的方向和密切程度的特征数。用r表示。如r为正值，则表明为正相关；r为负值，则表明为负相关。其区间为〔+1,-1〕。表达式：

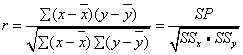
相关系数Xiangguan xishu

表示两个变量间相关程度的量数。相关系数有许多种，如积差相关系数、等级相关系数和质量相关系数等。它们各自适用于不同的数据资料。积差相关系数：表示两列连续的正态分布的变量之间相关程度的量数。计算公式为：

式中 r——积差相关系数；SX——X变量的标准差；SY——Y变量的标准差。积差相关系数的取值在-1.00至+1.00之间。取值的正负号表示相关的方向，正值表示正相关，即一个变量随另一个变量增大（减小）而增大（减小）；负值表示负相关，即一个变量随另一个变量增大（减小）而减小（增大）。r的绝对值的大小表示相关程度的大小，绝对值越大，则相关程度越大。等级相关系数：表示两个等级或顺序变量之间相关程度的变量。计算公式为：

式中 rR——等级相关系数；Di——第i对数据的等级之差。以上的公式实际上可以由积差相关系数公式导出，且当有相同等级出现时应对公式进行校正。等级相关系数的取值范围也在-1.00至+1.00之间。两列连续变量若不满足正态分布，将其转化为等级分数，也可以用等级相关系数表示相关程度。

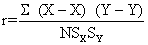
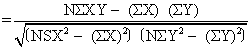
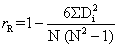
相关系数coefficient of correlation

是指衡量两个随机变量之间线性相关程度的指标。用ρ表示总体相关系数，x、y是两个随机变量，则ρ可用如下公式定义为：

如果总体未知，ρ无法计算，则可以利用样本值给出ρ的一个估计γ。定义样本相关系数

其中：

，称为X与Y的样本协方差。包括：

，称为X的样本方差；

，称为Y的样本方差。由于S_xy,S_x²和S_y²分别是cov(x,y),δ_x²和δ_y²的无偏估计量，所以样本相关系数γ是总体相关系数ρ的一个无偏估计量。由相关系数的计算公式易得其取值范围为： |γ|≤1。当r>0时，称X为Y正相关； 当r<0时，称X与Y负相关； 当r=0时，称X与Y不 （线性）相关。当|r|=1时，X与Y完全 （线性） 相关。此时，所有观察值都落在一条直线上。|γ|越接近1,X与Y之间（线性） 相关程度越高。这仅是两个变量之间的线性相关，又称简单相关，所得出的相关系数也只是简单相关系数。实际上，在经济活动中，两个变量之间的相关程度总要受到其他有关变量的影响。一般地，在考察多个变量Y,x₁,x₂，…，x_k之间的关系时，如果其他变量不变，仅仅考虑Y与x_i (i=1,2，…，k)之间的关系，这种相关叫偏相关。衡量偏相关程度的指标，就是偏相关系数。在偏相关中，根据固定变量数目的多少，可分为零阶偏相关，1阶偏相关，……(k-1) 阶偏相关。零阶偏相关就是简单相关。

γ_01,2是剔除x₂的影响之后，Y与X₁之间的偏相关程度的度量。式中，γ₀₁,γ₀₂,γ₁₂分别是Y,x₁,x₂它们两两之间的简单相关系数。相关系数可以剔除变量单位对衡量变量之间相关程度的影响。但它也有不足之处：它只是能说明x,y之间是否存在线性关系； 同时它也无法表明是x影响y，还是y影响x，或是x,y相互影响，或是另外因素引起了x,y共同变化。

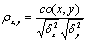
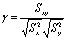
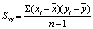
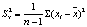
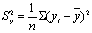
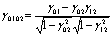
相关系数Correlation Index

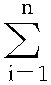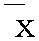概率论中表示两个随机变量δ和η之间线性联系程度的一个数值，其绝对值在0与1之间。δ和η之间的线性联系程度越大，相关系数的绝对值则越接近于1。当δ和η满足线性关系式aδ+bη=c时，其中，a、b和c为参数，相关系数的绝对值为1；当δ和η的变化为同一方向时，相关系数为正，反之则为负。通常在得到(δ,η)的n组观察值(x₁,y₁),(x₂,y₂)，…，(x_n,y_n)后，可用下式中的γ来估计δ和η的相关系数：γ=[(x_i-)(y_i-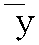)]　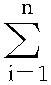(x_i-x)²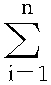(y_i-y)²。其中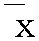，和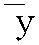分别为{x_i}和{y_i}的算术平均值。

相关系数

衡量两个或两个以上经济变量之间相互关系的密切程度的指标。相关系数的取值范围介于正负1之间。相关系数的绝对值越接近1，说明经济变量之间的相关程度越大。当相关系数的绝对值等于1时，经济变量之间的关系是一种确定性的、一一对应的关系，这时变量之间的关系称为“完全相关”。当相关系数为0时，经济变量之间的相关程度最小，变量之间不存在任何关系，称为“完全不相关”或“零相关”。一般情况下，相关系数的绝对值在0和1之间，说明经济变量之间存在一定的相关关系。当相关系数为正数时，变量之间存在正相关，即变量是同方向变化的，它们同时增加或同时减少；当相关系数为负数时，变量之间存在负相关，即变量是异向变化的，即此增彼减或此减彼增。衡量两个经济变量之间相互关系的密切程度的相关系数，称为“简单相关系数”。衡量多元回归模型中因变量与每个自变量之间单独的相关程度的相关系数，称为“偏相关系数”。衡量多元回归模型中因变量与所有自变量之间相关程度的相关系数，称为“多重相关系数”。

相关系数

描述变量间线性相关关系密切程度的统计分析指标。相关系数(r)数值的范围在-1和+1之间。r>0为正相关，r<0为负相关，r=0时，说明变量之间无线性关系。r的绝对值越大，相关程度越高。两个变量之间的相关程度，一般划分为4位，即无相关(|r|<0. 3)、低度相关(0. 3≤|r|<0. 5)、显著相关(0. 5≤|r|≤0. 8)和高度相关(|r|>0. 8)。相关系数的计算公式为： r=

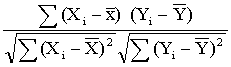
式中，X_i为自变量的标志值，i=1,2，…n;X为自变量的平均值；Y为因变量数列的标志值；Y为因变量数列的平均值； n为自变量数列的项数。这种计算相关系数的方法称为积差法，它可直接根据给定资料计算，而不经过回归分析，保证了相关系数计算与应用的独立意义。

相关系数

一种对两个随机变量之间内部关联程度的测度。其计算最早由英国人Kart Pearson提出，故相关系数亦可称为“普尔申系数”。其计算公式：

式中，r为x、y的简单相关系数；σx、σy分别为x、y的标准差；σxy为xy的协方差。
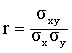
另一个英国人SPearman从 “普尔申系数” 出发，提出了关于两个随机变量等级变动之间的关联程度的测度公式，即等级相关系统，亦称作 “Spearman系数”。其计算公式：

式中，r为等级相关系数； n为成对变量的个数； d为成对变量的等级之差。
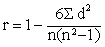
第三种常见的相关系数是复相关系数，在回归分析中使用。它反映被解释变量与多个解释变量之间内在关系的密切程度。一般用R表示，是拟合优度的平方根。
相关系数的数学性质：
❶相关系数介于-1和1之间，即，|r|≤1。
❷如果r>0，则两个变量呈正相关关系，即两个变量同方向变动； r<0，则两个变量呈负相关关系，即两个变量逆方向变动。
❸|r|=1，称为完全相关，表明两个变量之间存在确定的线性函数关系。
❹|r|=0，称为完全不相关，表明两个变量之间不存在任何关系，是相互独立的。
❺|r|越大则两个变量的关系越密切。一般认为，在大样本条件下，如果有|r|≥0.85，则认为两个变量之间存在强相关关系； 如0.45≤|r|≤0.85，则认为两个变量之间存在中等相关关系；如果“临界值”≤|r|≤0.45，则认为两个变量之间存在弱相关关系。

相关系数correlation coefficient

一种对两个随机变量之间内部关联程度的测度。其计算最早由英国人KartPearson提出，故相关系数亦可称为“普尔申系数”。其计算公式：

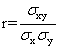
式中，r为x、y的简单相关系数；σ_x、σ_y分别为x、y的标准差；σ_xy为xy的协方差。
另一个英国人Spearman从“普尔申系数”出发，提出了关于两个随机变量等级变动之间的关联程度的测度公式，即等级相关系统，亦称作“Spearman系数”。其计算公式：

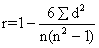
式中，r为等级相关系数；n为成对变量的个数；d为成对变量的等级之差。
第三种常见的相关系数是复相关系数，在回归分析中使用。它反映被解释变量与多个解释变量之间内在关系的密切程度。一般用R表示，是拟合优度的平方根。
相关系数的数学性质：
❶相关系数介于-1和1之间，即，|r|≤1。
❷如果r>0，则两个变量呈正相关关系，即两个变量同方向变动；r<0，则两个变量呈负相关关系，即两个变量逆方向变动。
❸|r|=1，称为完全相关，表明两个变量之间存在确定的线性函数关系。
❹|r|=0，称为完全不相关，表明两个变量之间不存在任何关系，是相互独立的。
❺|r|越大则两个变量的关系越密切。一般认为，在大样本条件下，如果有|r|≥0.85，则认为两个变量之间存在强相关关系；如果0.45≤|r|≤0.85，则认为两个变量之间存在中等相关关系；如果“临界值”≤|r|≤0.45，则认为两个变量之间存在弱相关关系。

相关系数

用来表示两个现象之间相关程度的量的统计分析指标。一般用γ来表示。相关系数只是一个比率，不是相关量数的等单位度量，无单位名称，也不是相关的百分数。γ的数值位于+1.00～-1.00之间，一般要取小数点后两位来表示，以便更精确地显示其相关程度。相关系数的正、负号只表示相关的方向，其绝对值表示相关的程度，所以γ=+1.00或-1.00，都是完全相关，只不过方向相反，绝不能说前者的相关系数比后者高。又因为γ不是等单位的度量，因而不能说相关系数0.70是0.35的两倍，只能说前者所表示的变量间的相关程度比后者更为密切或更高，同样，也不能说相关系数从0.70到0.80与从0.30到0.40增加的程度一样大。对于相关系数的价值如何解释，统计学界尚存争议，但通常作如下解释：γ在0.00至±0.30之间，表示无相关或微相关；γ在±0.30至±0.50之间，表示确有关系，称之为切实相关；γ在±0.50至±0.80之间，表示相关程度较高，称之为显著相关；γ在±0.80至±1.00之间，表示相关程度很高，称之为高度相关。计算相关系数的方法，通常采用积差相关法、等级相关法、点双列相关法等。

相关系数

测度现象之间相关关系密切程度和方向的分析指标。一般用“r”表示，变动范围在-1与+1之间，r数值在0.3以下为无相关；0.3～0.5之间为低度相关； 0.5～0.8之间为显著相关；0.8以上为高度相关。它可以用积差法或别的方法计算。其计算公式如下：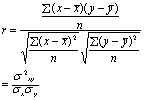

式中： x为自变量； 为自变量的平均数；y为因变量；ȳ为因变量的平均数； n为相关变量的项数；σ²_xy为两种变量的离差乘积的平均数； σ_x为自变量x的标准差； σ_y为因变量y的标准差。

相关系数correlation coefficient

参见“相关分析”。

相关系数

描述两个变量之间线性相关关系密切程度和方向的数量指标。总体的相关系数通常是通过样本相关系数进行估计的。其一般公式如下：

式中： r为样本相关系数，r2为决定系数，x为目变量，y为因变量。相关系数的数值介于-1与+1之间。正值为正相关，表示y有随x的增加而增加的趋向； 负值为负相关，表示y有随x的增加而减少的趋向。r=0，为零相关，表示y的变化与x无关，没有线性关系。r=±1，为完全相关，表示所有的点都在回归直线上。当r接近±1，表示强相关； r接近0，表示弱相关。计算相关系数的样本数据必须相当多，才能用r来估计总体的相关系数。相关程度的显著性，可通过相关系数检验表进行检验。相关系数还可采用另外的公式计算。在已计算出变量的平均值的情况下：

在已有平均数及均方差的情况下：

为了避免在计算过程中使用平均数，可用下式计算：

这些公式计算结果是相等的，可根据掌握的不同资料选用。

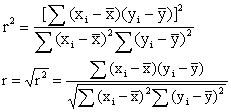
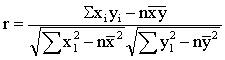
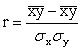
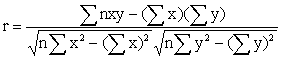
相关系数correlation coefficient

描述变量之间线性相关程度的数量指标。常用r表示，其值在-1到+1之间。当-1≤=r≤0时，变量间的变化方向相反，即当一个变量增大当r=0时，变量间没有相关，称零相关；当0< r≤1时，变量间的变化方向一致，即两个变量同时增大或减少，称正相关；当r=1或r=-1时，变量之间呈一定的比例变化，称完全相关。针对不同的条件(数据的种类、分布形式)，相关系数被分成多种类型，有不同的计算方法：(1)按数据各类分有：简相关系数、偏相关系数、自相关系数和组内相关系数； (2)按分布的形式分有：积差相关系数、列联相关系数、点双列相关系数、双列相关系数、斯皮尔曼相关系数等。

相关系数correlation coefficient

统计分析中度量不同变量间关联程度和方向的统计指标。用r表示。相关系数的取值范围一般为(-1,+1)。相关系数的绝对值越接近于1，表示两个变量之间联系程度越大。相关系数小于0时，称为负相关；大于0时，称为正相关；等于0时，称为零相关。依据相关现象之间的不同特征，统计指标的名称亦有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数（相关系数的平方称为决定系数或判定系数）；反映两变量间曲线相关关系的统计指标称为非线性相关系数；将反映多元线性相关关系的统计指标称为复相关系数等。

相关系数

衡量事物之间相关程度的统计指标。数值大小反映关联程度大小，符号代表关联方向。