直线和普遍二次曲面的相关位置zhixian he pubian erciqumian de xiangguan weizhi

设二次曲面

F (x,y,z) ≡φ (x,y,z) +

2ux+2vy+2wz+d= 0 (1)

φ (x,y,z) ≡ax²+by²+cz2+2fyz+ 2gzx+ 2hxy.l是过P₀ (x₀,y₀,z₀)方向余弦为λ,μ,γ的直线

x =x₀ +λt,y =y₀ +μt,z = z₀ +γt,　(2)

将 (2)代入 (1)，得t的二次方程

Qy²+2Rt+S=0　(3)

Q=φ (λ,μ,γ)

R=λ(αx₀+hy₀+gz₀+u)+μ (hx₀+by₀+fz₀+v)+
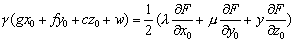
S=F (x₀,y₀,z₀).
当Q≠0时，若R²-QS>0，则 (2)与 (1)有两个不同的交点，(2)叫做(1)的割线；若R²-QS=0，则 (2)与 (1)有一个交点 （看作两个点的重合）,(2) 叫做 (1) 的切线； 若R2-QS<0，则 (2) 与(1) 无交点，(2) 叫做 (1) 的离线.
当Q=0,R≠0时，(3)的一个根趋于无穷，(2)叫做 (1) 的一个交点趋于无穷的割线.
当Q=R=0,S≠0时，(3)的两根趋于无穷，(2)叫做 (1) 的渐近线.
当Q=R=S=0时，t的任何值都适合方程(3)，直线 (2) 完全在曲面 (1) 上，故 (2) 叫做 (1) 的母线.
注意： 曲面F (x,y,z) = 0上的一点 (x₀,y₀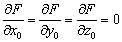时，此点叫做奇异点，在奇异点处R= 0.