直线和平面平行的性质定理zhixian he pingmian pingx-ing de xingzhi dingli

定理1 若一条直线和一个平面平行，经过这条直线的一个平面和这个平面相交，则这条直线就和交线平行.

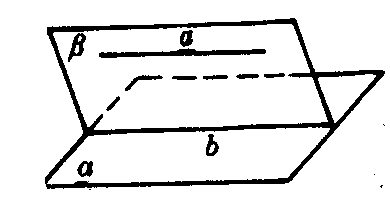
图1

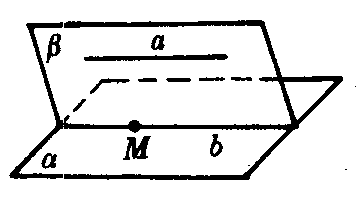
图2

如图1，若a∥a,a⊂β,a∩β=b.则a∥b.
这个定理为我们提供了一种证明两条直线平行的办法.
定理2 若一条直线和一个平面平行，则过已知平面内任一点和已知直线平行的直线只有一条，而且这条直线必在已知平面内.
如图2，若a∥a,M∈a,M∈b,a∥b，则b⊂a，且b只有一条.
设过a和M的平面为β，实际上b是a和β的交线.
这个定理在添加辅助线时常用到.
由上面的定理可推出下面的性质：
❶若一条直线与一个平面平行，则夹在这条直线和平面间的平行线段相等.

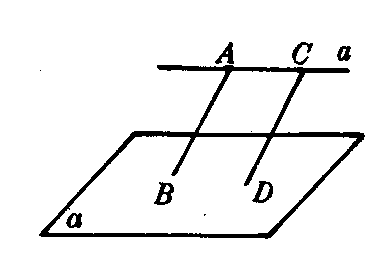
图4

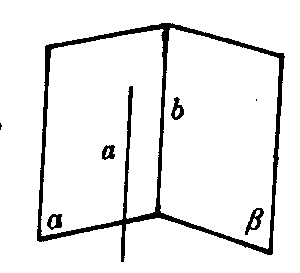
图5

如图3，若a∥a,AB∥^CD,A∈a,B∈a,C∈a,D∈a.则AB=CD.

❷若一条直线与两个相交平面都平行，则这条直线与这两个平面的交线平行.
如图4，若a∥a,a∥β,a∩β=b，则a∥b.

❸过平面外一点且平行于这个平面的所有直线，都在经过该点且平行于这个平面的一个平面内.
如图5，若Aa,A∈β,a∥β,A∈a,a∥a，则a⊂β.