游程检验

依时间或其他顺序排列的有序数列中，具有相同的事件或符号的连续部分称为一个游程。在一个游程中的事件或符号的个数称为该游程的长度。例如在以下的两个符号序列中，
(1) ++++------
(2) --+-+++--+若以r表示游程的个数，l表示某游程的长度，则序列(1)的r=2,l依次为4和6；序列(2)的r=6,l依次为2,1,1,3,2,1。设样本序列中，所有观察值只能分为互不相容的两类事件，一类观察值的个数为n₁，另一类为n₂,n₁+n₂＝n。游程检验包括游程个数检验和游程长度检验。二者均可用于检验序列中两类事件发生过程的随机性，游程个数检验还可用于两样本的比较。
序列的随机性检验 目的是推断序列中两类事件的发生过程是否随机的。有游程个数检验与游程长度检验两种方法。
游程个数检验 它是根据样本序列中，n₁、n₂与r值的大小来推断两类事件的发生过程是否随机的。检验假设H₀为两类事件的发生是随机的，备择假设H1为两类事件的发生不是随机的。基本思想是： 若由H₀ 的总体作随机抽样，当n₁与n₂一定时，r值不会太大也不会太小；若r值太大或太小，将怀疑此样本不是来自H₀的总体。当求得r值后，可从游程检验用r界值表(表1)查得由H0中抽得此r的概率P。对于给定的检验水准α，若r≤“rα的下界”或r≥“rα的上界”，则P≤α，于是按α水准拒绝H0，接受H1；若“rα的下界”α，于是不拒绝H0。
当n₁或n₂超出表1范围时，可用式(1)将游程个数检验变换为u检验，然后查u界值表得P值，按所取检验水准作出推断结论。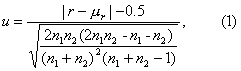

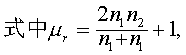分式的分母为r的标准误。
此外，有些序列的观察值是用数值的大小表示的，可以通过中位数法将其变换为两类事件，然后按游程个数检验推断其随机性。如例2为某病病死率的动态数列，可先求得其中位数M，再将各观察值之大于M者标以“+”号，小于M者标以“-”号，等于M者弃去不计；最后按符号序列求得游程个数r，查表1得P值，按所取检验水准作出推断结论。
例1 某村发生某种地方病。住户沿一条溪水排列，调查结果对9家病户标以“+”号，17家非病户标以“-”号。问病户分布是否随机的？

H₀: 病户排列是随机的，
H₁: 病户排列非随机的。
α=0.05。
计得r=14，今n₁＝9,n₂＝17，查表1得P>0.05，按α=0.05水准不拒绝H0，故可以认为此病的病户分布很可能是随机的，尚看不出有聚集性。

表1 游程个数检验用r界值表
上行： P(1)=0.05，下行： P(2)=0.05,n₁≤n₂

n1

n2

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

5

3～9 2～10

3～10 3～10

3～10 3～11

3～11 3～11

4～11 3

4～11 3

4 4

4 4

4 4

5 4

5 4

5 4

5 4

5 5

5 5

5 5

6

3～11 3～11

4～11 3～12

4～12 3～12

4～12 4～13

5～12 4～13

5～13 4～13

5～13 4～13

5～13 5

5～13 5

6 5

6 5

6 5

6 5

6 6

6 6

7

4～12 3～13

4～13 4～13

5～13 4～14

5～13 5～14

5～14 5～14

6～14 5～14

6～14 5～15

6～14 5～15

6～15 6～15

6～15 6

7～15 6

7～15 6

7～15 6

7 6

8

5～13 4～14

5～14 5～14

6～14 5～15

6～15 5～15

6～15 6～16

6～15 6～16

7～16 6～16

7～16 6～16

7～16 6～17

7～16 7～17

8～16 7～17

8～16 7～17

8～17 7～17

9

6～14 5～15

6～15 5～16

6～15 6～16

7～16 6～16

7～16 6～17

7～17 7～17

8～17 7～18

8～17 7～18

8～17 7～18

8～18 8～18

8～18 8～18

9～18 8～18

10

6～16 6～16

7～16 6～17

7～17 7～17

8～17 7～18

8～17 7～18

8～18 7～18

8～18 8～19

9～18 8～19

9～19 8～19

9～19 8～20

9～19 9～20

11

7～17 7～17

8～17 7～18

8～18 7～19

8～18 8～19

9～19 8～19

9～19 8～20

9～19 9～20

10～20 9～20

10～20 9～21

10～20 9～21

12

8～18 7～19

9～18 8～19

9～19 8～20

9～19 8～20

10～20 9～21

10～20 9～21

10～21 9～21

10～21 10～22

11～21 10～22

13

9～19 8～20

9～20 9～20

10～20 9～21

10～21 9～21

10～21 10～22

11～21 10～22

11～22 10～23

11～22 10～23

14

10～20 9～21

10～21 9～22

11～21 10～22

11～22 10～23

11～22 10～23

12～22 11～23

12～23 11～24

15

11～21 10～22

11～22 10～23

11～22 11～23

12～23 11～24

12～23 11～24

12～24 12～25

16

11～23 11～23

12～23 11～24

12～24 11～25

13～24 12～25

13～25 12～25

17

12～24 11～25

13～24 12～25

13～25 12～26

13～25 13～26

18

13～25 12～26

14～25 13～26

14～26 13～27

19

14～26 13～27

14～27 13～27

20

15～27 14～28

摘自 山内二郎： 统计数值表，298,JSA-1972
例2 某病病死率逐年排列如下，此20年间病死率的变化是否随机的？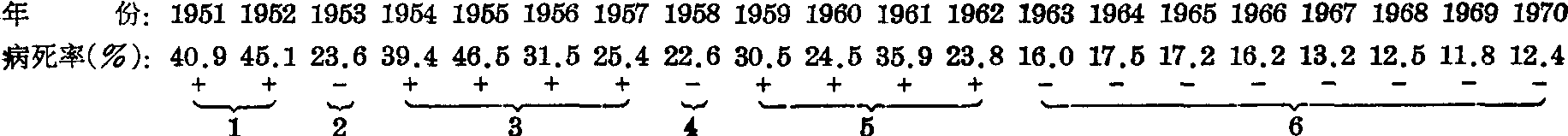

H₀: 逐年病死率变化是随机的，
H₁: 病死率的变化不是随机的。
a=0.05。
求中位数：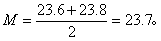

M的病死率有10个，均标以“+”号。计游程个数： r=6。今n₁＝10,n₂＝10，查表1得P<0.05，按a=0.05水准拒绝H₀，接受H₁，故可认为此病病死率在1951～1970年间的变化不是随机的，出现了几个持续的过程。1954～1957年和1959～1962年病死率持续较高，而1963～1970年则持续较低。
游程长度检验 它是根据样本含量n及序列中最长游程的长度l来推断两类事件的发生过程是否随机的。检验假设H₀为两类事件的发生是随机的，备择假设H₁为两类事件的发生不是随机而是有升降倾向的。基本思想是： 由H0的总体作随机抽样，当n一定时，l值不会太大，若太大将怀疑此样本不是来自H₀的总体。当求得l值后，可从游程长度检验用l界值表(表2为简表，仅列出大于或等于界值时相应的P值)查得P值，再按所取检验水准作出推断结论。
有些序列的观察值是用数值大小表示的，如例2，可以先变换为符号序列，再进行游程长度检验。变换的方法是： 确定序列中相邻两观察值之差的符号。若后者大于前者记“+”号，反之记“-”号，相邻两值相等时，删去其一，使序列中没有相邻的等值。样本含量n亦相应减少。

表2 游程长度检验用l界值简表（单侧）

n	P<0.05	P<0.01
5	4
6～7 8～9 10～26 27～34 35～100	4 5 5 6 6	5 5 6 6 7

摘自 山内二郎：統計数值表，304,JSA-1972
例3 用游程长度检验例2的随机性。
H₀: 同例2,
H₁: 病死率的变化不是随机而是有下降倾向的。
单侧α=0.05。
根据逐年病死率的变化（计相邻两年病死率之差的符号），得下列符号序列：
+ - + + - - - + - + - - + - - - - - +此序列有19个符号，n=20，最长游程的长度l=5，查表2得P<0.05。按α=0.05水准拒绝H₀，接受H₁。1964～1969年间游程长度最长，且符号为“-”，可认为此阶段病死率有下降趋向。
两样本的比较 本法把游程个数检验用于两样本的比较，目的是推断两样本分别代表的两总体分布是否相同。如果结论是分布不同，本法还不能肯定是位置不同、变异度不同还是偏度不同。
方法步骤： 将两样本的观察值混合由小到大排列，并在各观察值下注明其所属样本，比如属第一样本者记以X，属第二样本者记以Y。计算序列中的游程数r，查表1得P值，或按式(1)计算u值，再查u界值表得P值，按所取检验水准作出推断结论。
若两样本中有一个或几个观察值相等，计算r的方法是将相等观察值下的X与Y作两种排列： 一种是使游程数最小，记作r′；另一种是使游程数最大，记作r″。r=(r′+r″) /2。若相等观察值只在同一样本内时，并不影响r值。例如序列“10 14 14 14 16”中，10属于X,16属于Y，其中3个14，有2个属于Y,1个属于X 。于是最小游程数的排列法为XXYYY,r′=2；最大游程数的排列法为XYXYY,r″=4，故r=(2+4)/2=3。
例4 两类胃癌（高分化腺癌与未分化癌）各10例，术后生存月数如下。问两组间有无差别？
高分化腺癌(X): 10,14,19,36,47,53,56,94,141,169
未分化癌(Y): 6,6,7,9,14,14,16,25,37,46
H₀: 两总体分布相同，
H₁: 两总体分布不同。
α=0.05。
将两组数据统一由小到大排列(相同数据14的X、Y作两种排列，上行的r值最小，下行最大):

6,	6,	7,	9,	10,	14,	14,	14,	16,	19,	25,	36,	37,	46,	47,	53,	56,	94,	141,	169
Y	Y	Y	Y	X	X Y	Y X	Y Y	Y	X	Y	X	Y	Y	X	X	X	X	X	X

由以上序列可得r′=8,r〃=10。于是得r=(8+10)/2=9。查r界值表，当n₁＝n₂＝10时，P>0.05，按α=0.05水准不拒绝H₀，故不能认为两类胃癌生存期的分布不同。