混杂设计confounded design

主动混杂一部分次要效应以缩小区组容量提高主要目标效应精确性的试验设计方法。完全实施多因素试验中，每个重复内处理数较多，土壤差异及其他随机误差也相当大。解决的办法是将一个重复的实验单元按照一定规则划分为二个或二个以上区组，每个区组内只包含全部实验单元的一部分，成为不完全区组。划分区组后一部分因素效应或交互作用效应与区组效应相混杂，未与区组效应混杂的其他效应，则因区组容量缩小，区组内随机误差变小，从而提高了精确度。在一个多因素试验中各因素的重要性随研究目的而有区别，必须将次要效应与区组效应相混杂才能收到混杂设计的预期效果。若将主要研究的效应与区组效应相混杂是得不偿失的。混杂设计最适于在山区及稻田等应用。
二水平多因素混杂设计试验 在肥料试验中经常进行2×2×2的试验。若嫌一个重复8个小区过多，可采用混杂设计将每个重复划作区组容量为4的两个区组，需混杂何种效应可制成混杂效应表，A、B、C代表肥料因素并表示施肥，O代表不施肥。

2×2×2混杂效应

因素及水平代号			混杂的效应
A	B	C	A	B	C	AB	AC	BC	ABC
0 A	0 0	0 0	- +	- -	- -	+ -	+ -	+ +	- +
0 0	B 0	0 C	- -	+ -	- +	- +	+ -	- -	+ +
A A	B 0	0 C	+ +	+ -	- +	+ -	- +	- -	- -
0 A	B B	C C	- +	+ +	+ +	- +	- +	+ +	- +

混杂的效应项下的A表示A因素已混杂，分区组的方法为将4个“+”号处理放在同一区组，4个“-”号的放另一区组，即将因素A与区组混杂。交互作用的混杂方法也以“+”、“-”号分区组。四个因素以上也有相应的混杂效应表。一般的二水平多因素混杂试验亦需遵守设置重复，局部控制及随机排列三项原则。如以ABC高阶交互作用与区组混杂，则线性数学模型为

y_jklm=μ+ρ_j+A_k+B_l+C_m
+(AB)_kl+(AC)_km (1)
+(BC)_lm+ε_jklm

式(1)中 μ为总体平均，ρ_j为区组效应，A_k、B_l、C_m、(AB)_kl、(AC)_km、(BC)_lm为各种肥料因素主效应与交互作用效应，ε_jklm为随机误差。高阶交互作用效应(ABC)_klm因与区组效应相混杂，故式(1)中无这一项。凡与区组效应相混杂的效应都不列入线性数学模型。
部分混杂试验 每个重复都混杂不同的效应，在某一重复中被混杂的效应可在其他重复中得到考察，部分混杂设计取得缩小区组容量的优点，又可考察全部交互作用效应。如果有四次重复的试验，每次重复混杂不同的效应，在另三个重复中仍可考察被混杂的效应。这时式(1)即成为式(2)的形式
y_jklm＝μ+ρ_j+A_k+B_l+C_m+(AB)_kl
+(AC)_km+(BC)_lm (2)

+(ABC)_klm+ε_jklm
计算平方和与自由度的方法需按式(2)进行。
不设重复的三水平混杂试验 3×3×3析因试验是应用混杂设计最多的试验。一些国家肥料试验网组织都做过这种氮磷钾三要素试验。每个因素为三个水平，一般都采用等间距水平，三个水平的效应可分解为直线效应与曲线效应两部分。例如氮肥施用量分为每公顷0、75、150千克有效成分，分别记作N₀、N₁及N₂。效应为直线时N₂—N₁应等于N₁—N₀，故N₂—N₀可度量直线效应。如N₂—N₁≠N₁—N₀，斜线y(图1)必然曲折，因此N₂—2N₁+N₀可度量曲线效应。

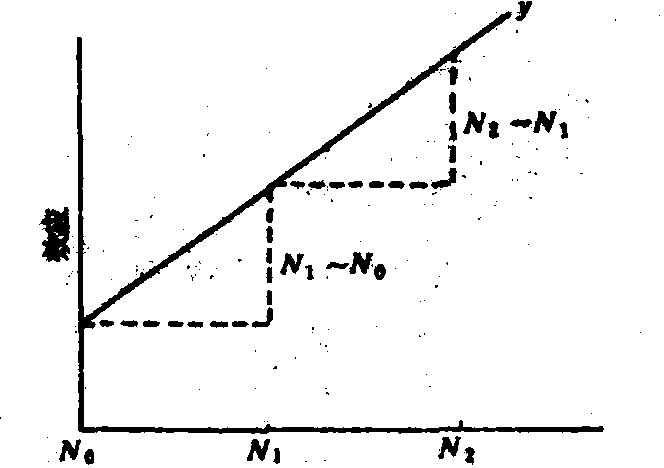
图1 直线效应示意图

3×3×3试验共27个处理组合，采用混杂设计时大多划作区组容量为9的三个区组，并混杂高阶交互作用。现代的混杂分区组方法都利用正交表L₂₇(3¹³)（见正交设计），从表中的9、10、12、13列中随机选出一列，每列中都有1、2、3三个水平各9次，将该列中相同水平的处理组合作为一个区组，就完成了区组的划分。各处理在区组内须随机排列。这类试验不设重复，但有三个区组，其线性数学模型为

y_jklm＝μ+ρ_j+(AL)_k+(A_c)_k+(BL)_l

+(B_c)_l+ (C_L)_m+(C_c)_m (3)+
(A_LB_L)_kl+(A_LC_L)_km
+(B_LC_L)_lm+ε_jklm
式(3)中 μ为总体平均、ρj为区组效应、A、B、C为三个肥料因素，下标L、C分别表示直线效应与曲线效应。(A_LB_L)kl、(A_LC_L)km、(B_LC_L)lm为二因素的线性交互作用效应、ε_jklm为随机误差。由于模型中无高价交互作用项及曲线效应有关的两因素交互作用，故这种设计的剩余自由度竟高达15，可以用方差分析进行显著性检验。
设重复的三因素三水平混杂设计 不设重复的3×3×3混杂设计虽可进行方差分析，但其剩余均方，并非真正的误差均方，因此也有设置重复并采用部分混杂设计（一般只设二次重复），每次重复分别混杂高阶交互作用的一部分效应。这时的线性数学模型为：

y_jklm=μ+ρ_j+A_k+B_l+C_m+(AB)_kl
+(AC)_km+(BC)_lm (4)
+ (ABC)_klm+ε_jklm

也可将A、B、C因素分解为直线效应与曲线效应两项，每个二因素交互作用都可分解为直线×直线、直线×曲线、曲线×直线、曲线×曲线交互作用。由于与区组效应相混杂，高阶交互作用效应的计算需作校正。
混杂裂区试验 裂区试验的二级因素有时为多个因素所构成，处理组合数较多，若将二级因素用混杂设计划分为二个区组，则可减少在每个整区中的裂区数目，从而提高试验的准确性。例如一级因素为品种，二级因素为氮磷钾二水平三因素的8个处理组合。如用混杂设计混杂氮磷钾高阶交互作用，则每个品种整区只需划为4个裂区，这个试验的线性数学模型为

y_jklmn＝μ+ρ_j+V_k+(ε₁)_jk+A_l
+B_m+C_n+(VA)_kl+(VB)_km
+ (VC)_kn+ (AB)_lm+(AC)_ln+ (5)
(BC)_mn+(VAB)_klm+(VAC)_kln
+(VBC)_kmn+(ε₂)_jklmn

式(5)中 V_k为品种，(ε₁)_jk及(ε₂)_jklmn为误差 Ⅰ与误差Ⅱ，其余各项为品种与三种肥料之间的交互作用效应。因已与区组效应相混杂，式(5)中无(ABC)_lmn及(VABC)_klmn两项高阶交互作用效应。并据此进行平方和及自由度分解后作方差分析。
拟拉丁方试验 用混杂方法于拉丁方试验以缩小拉丁方边长的试验。可以兼收到控制两个方向土壤差异及减少试验工作量的双重效果。例如氮磷钾三因素两水平共8个处理组合，如用8×8拉丁方需重复8次，共64个实验单元。如纵横两个方向分别混杂氮磷钾高阶交互作用及一种二因素交互作用效应（如磷钾），则成为4×4拉丁方。为了增加必要的误差自由度通常增设一个或二个拟拉丁方如图2所示。

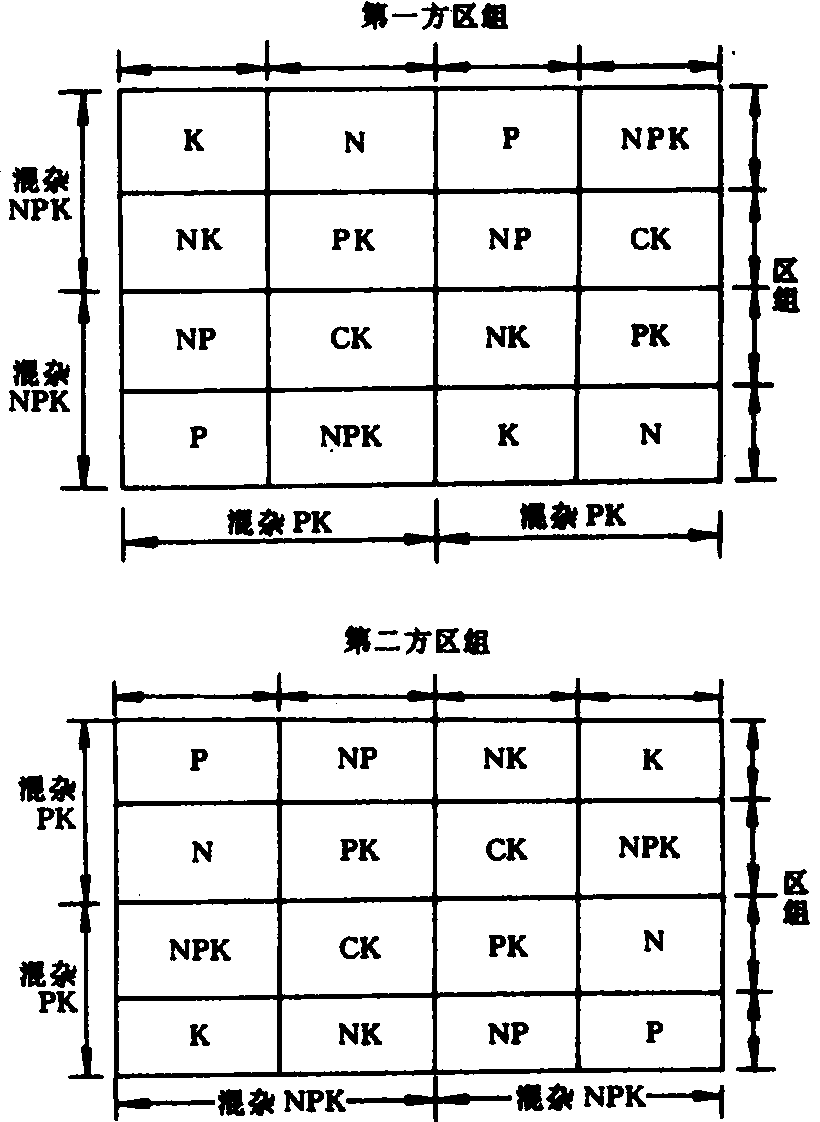
图2 二块4×4拟拉丁方试验田间排列示意图

该试验的线性数学模型为：
y_ijklmn＝μ+V_i+ρ_j+λ_k+A_l+B_m+Cⁿ
+(AB)_lm+(AC)_ln+ε_ijklmn(6)
式(6)中 Vi为拉丁方间效应，ρ_j、λk分别为行及列区组效应，A_l、B_m、C_n为氮磷钾三种肥料效应，(AB)_lm、(AC)_ln为氮磷氮钾交互作用效应，ε_ijklmn为随机误差，磷钾及氮磷钾交互效应与区组效应混杂故式(6)中无这两项。并据上式进行平方和与自由度分解后作方差分析。