混杂样本剖析与正常值范围估计

确定正常值范围必须以同质的正常人样本作基础，即使要结合病人（异常）样本分布，仍得划清正常样本与异常样本。但有时由于对影响因素的无知或疏忽，以及准确的鉴别诊断有困难，而使实际得到的是一个混杂样本；在卫生机构的日常工作中积累有大量的资料，就某项医学特征而言，本身就是混杂样本，因为它包含着正常与异常两部分； 又如医院检验方法改变，前后资料缺乏同质性，有时新旧资料的界限不清，这也是混杂样本。因此，从混杂样本中剖析出正常样本，不仅可有效地利用经常性医学检查资料作为确定正常值的依据，还可结合剖析所得的异常样本的分布特征，为确定理想的正常值范围、分析漏诊和误诊等问题提供有利条件。解决了混杂样本剖析问题，在确定正常值范围的调查中，由于条件限制，还可放宽对“正常人”的鉴别诊断，减少工作量。各种混杂样本剖析法中，以Gram-Charlier级数 (以下简称G-C级数)为模型的剖析法，具有广泛的适用性。
混杂样本剖析的基本思想如图1所示，图中实线为混杂样本分布曲线，虚线为剖析出的同质样本，即混杂样本的各组成部分的分布曲线。图(a)是将混杂样本剖析为两个同质样本，图(b)是剖析为三个同质样本。同理，根据影响因素的增多，还可剖析为更多的同质样本。混杂样本剖析的目的是求出这些同质样本的总体参数的估计值或分布，作为确定正常值范围的基础。

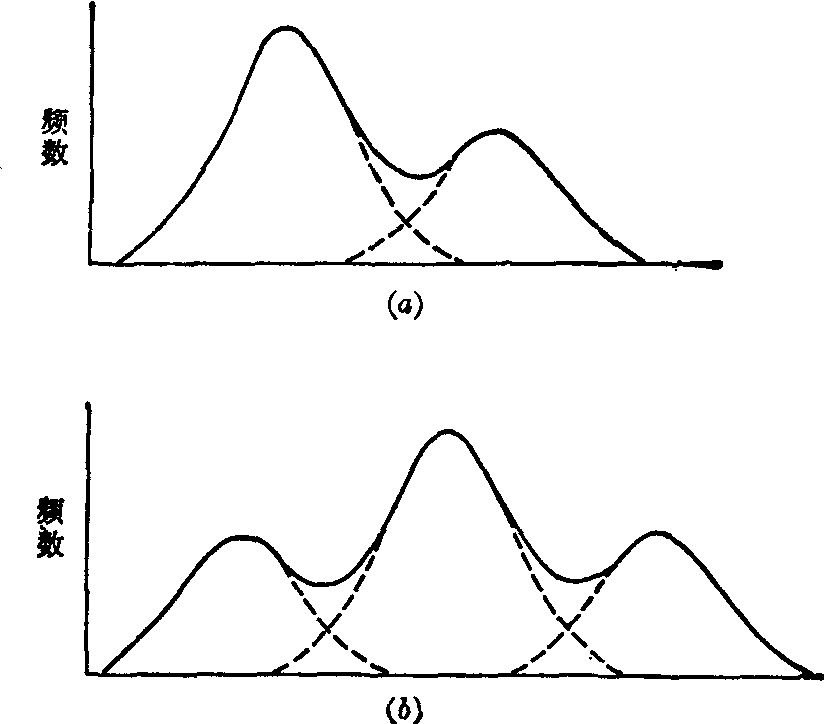
图1 混杂样本剖析示意

混杂样本剖析法 方法很多，都要先选定描述剖析的同质样本的数学模型，再按一定的求解方法估计总体参数。如有的以正态分布为模型，用图估法、矩法、极大似然法或最小二乘法等来估计参数； 有的以指数分布或Poisson分布为模型用矩法来估计参数；而H.F.Mar-tin等提出以G-C级数为模型（正态分布或偏态分布资料均可用），用非线性最小二乘法来估计参数。由于医学资料的分布型是多样的，而且经常是未知的，也难于预先确定其为何种分布。因此，以适用范围较广的G-C级数模型，在电子计算机上进行混杂样本剖析，常能得到满意的效果。一般说来，重叠比例(如图1(a)中重叠面积与较小同质样本面积之比)愈小，剖析的效果愈好。重叠比例过大，说明该指标的灵敏度和特异度较差，剖析的实际意义也是不大的。若估计两同质样本的含量比例相差过大，则应增加混杂样本总例数，使较小同质样本含量不致太少，则可提高剖析的效果。
G-C级数的简式为

此种函数的选择决定于混杂样本包含有几个同质样本。若异常样本分布在正常样本的两侧如图1(b)，函数至少为三个G-C级数相加；若异常样本仅在正常样本的一侧[如图1(a)]，函数至少为两个G-C级数相加，即

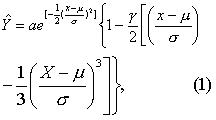
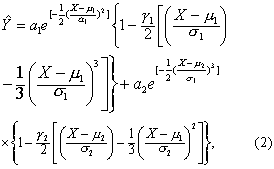
式中第一项与第二项分别描述两个同质样本。e为自然对数的底； X为频数表各组段的组中值，Y为相应组段的理论频数，可用来近似地描述混杂样本的分布；μ1与μ2分别为正常总体与异常总体的均数；σ1与σ2分别为正常总体与异常总体的标准差；γ₁与γ₂分别为正常总体与异常总体的偏度系数，偏度系数为0，则G-C级数为正态分布；a₁与a₂分别为对应于μ₁与μ₂的曲线高度（即频数）。G-C级数不是概率密度，有时在曲线一端Y会出现负值，但很小，实际应用中可以不计。
将混杂样本剖析为正常样本与一个异常样本，也就是确定式 (2) 中的八个参数： μ₁,μ₂,σ₁,σ₂,γ₁,γ₂,a₁,a₂。需要在初估值的基础上，经过计算机反复调试。可用非线性最小二乘准则求解，即

为最小。式中Y为混杂样本各组段的实际频数，Ŷ为其相应的理论频数， 1/Ŷ为权数，k为组段数， d为阻尼因子，⊿为两次估计参数迭代值之差，m为所估计参数的个数。当满足式(3)要求，可得一组“最优”参数解。这时，也是拟合的曲线“最优”，拟合优度检验的X2值必然最小，因此可通过X²值的大小来判断结果的优劣。X²值的算式为

当式(3)中的⊿小于容许误差，式(4)中的x2值小于给定的检验水准的界值时，求解过程结束。
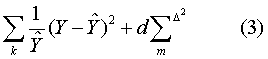
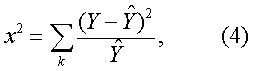
输入计算机的资料包括：
❶混杂样本的频数表，X的组段数k及总例数N。
❷μ₁,σ₁,γ₁;μ₂,σ2,γ₂; 混杂样本中两同质样本含量n₁与n₂的比值K等的初估值以及它们的容许误差等。当N与K已知时，即可推导出a₁与a₂ （公式从略）。
初估值的获得可以通过下列途径：
❶根据以往的经验或文献报道；
❷由已确诊的部分正常人和病人分别求出其均数、标准差s，偏度系数g作为相应的总体参数的初估值(但此法不能估计K);
❸从大的混杂样本中随机抽取部分人，用被研究指标以外的其他医学诊断手段，鉴别为正常与异常两部分，分别求出上述指标的初估值；
❹图估法（从略）等。初估值良好，可以缩减计算机的调试，容易得出满意的效果。
由混杂样本剖析出正常样本后，若正常样本为正态分布，则可用正态分布法或百分位数法确定正常值范围；若正常样本为偏态分布则可用百分位数法确定正常值范围；由于正常样本的曲线方程已获得，亦可用定积分确定正常值范围，结果更为准确，但手续较繁。
混杂样本剖析必须密切结合专业实际。例如应当剖析为几个同质样本是与对研究指标影响因素的多少相联系的； 析得的同质样本及确定的正常值范围必须是符合实际的。
正常值范围的估计与评价 在剖析出正常样本与病人样本后，就可把二者结合起来分析计算符合与失误的概率，平衡得失，选定正常值范围的适当界值，并评价其应用价值。
(1) 划分正常值范围时，符合与错划的概率。在确定正常值范围时，总是先选定正常人群(A₁)与病人人群(A₂)，他们的检查结果，按某一界值C划分，常常两组人中均会有的是阴性(D₁)，有的是阳性(D₂)。则
❶将正常人划为阴性是符合的，其概率记为P(D₁|A₁);
❷将正常人划为阳性是假阳性，其概率记为P(D₂|A₁);
❸将病人划为阳性是符合的，其概率记为P(D₂|A2);
❹将病人划为阴性是假阴性，其概率记为P(D2|A2)。上述条件概率如图2所示，其算式分别为：

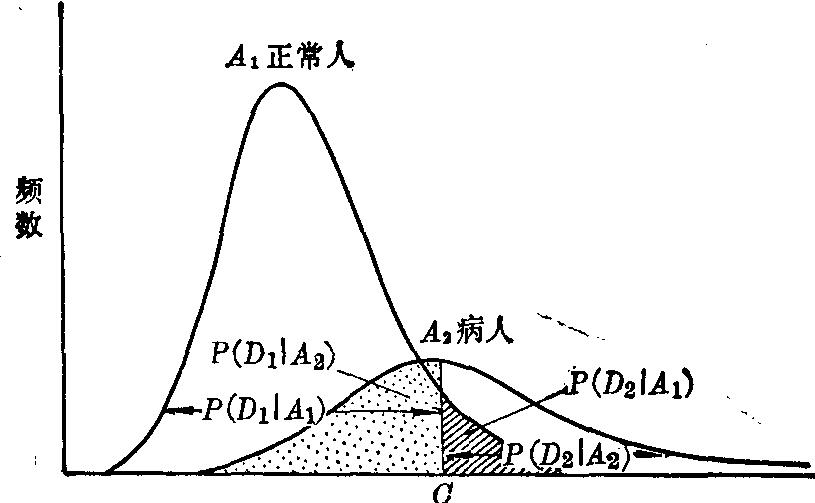
图2 符合与错划概率示意

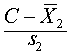式(7)中₂、s₂与g2分别为病人样本的均数、标准差与偏度系数。为标准正态（离）差u,φ(u)与φ(u)分别为标准正态分布的分布函数与密度函数，当u值确定后，均可由标准正态分布表查得。
(2)应用正常值范围作判别诊断时，符合与错判的概率。在判别诊断的实践中，总是将受检者的检查结果按某一界值C判定为阴性(D₁)与阳性(D₂)，然而常常是两者中均有的确属正常人(A₁)，有的确属病人(A₂)。则
❶阴性者确属正常人的诊断是符合的，其概率为P(A₁|D₁)，即将该界值用于诊断的阴性符合率；
❷阴性者确属病人是漏诊，其概率记为P(A₂|D₁)，即漏诊率；
❸阳性者确属病人的诊断是符合的，其概率记为P(A₂|D₂)，即将该界值用于诊断的阳性符合率；
❹阳性者确属正常人是误诊，其概率记为P(A₁|D₂)，即误诊率。这些后验概率不仅与前述划分正常值范围时的符合与错划的条件概率有关，而且与受检人群中正常人与病人的比例 （先验概率）P(A₁)与P(A₂)有关，根据Bayes公式分别得算式：

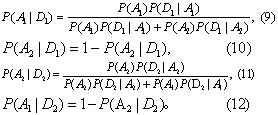
式(9)～(12)是评价正常值范围应用价值的实践标准。理想的是阴性符合率高，漏诊率低和阳性符合率高，误诊率低。这些都可根据要求加以平衡，当A₁与A2的比例一定的条件下，这只能通过移动C点，调整式(5)～(8)来实现(见条目“正常值范围”关于“选定百分范围”问题)。
由式(9)～(12)可见，正常人与病人的比例对确定正常值范围关系很大，比如人群中病人的比例很低，则误诊率会增高。但是这个比例可能经常变动，而且不同医疗机构也可能不同。为此，有条件的医院，宜用自己的正常值标准，而且应定期修订，只要注意经常性资料的积累，混杂样本剖析、确定正常值范围、计算后验概率等过程都可用系统的电子计算机程序来完成。
例 某医院用King法测得就诊病人1000例血清谷-丙转氨酶(SGPT)资料见下表第(1)、(2)栏，经用G-C级数模型剖析得“正常人”样本见第(1)、(3)栏，及病人样本见第(1)、(4)栏，前者代表无影响SGPT疾病的人，后者代表有影响SGPT疾病的人。有关参数的估计值：“正常人”样本a₁＝94.7,₁＝79.3,s1 =33.5, g₁＝0.96；病人样本a2=14.2,₂＝143.0,s₂＝57.8g₂＝1.38。试据此确定95%正常值范围，并对其作出评价。

1000例SGPT（单位）的实际频数与剖析理论频数

SGPT (1)	实际频数 (2)	理 论 频 数
		“正常人”样本 (3)	病人样本 (4)	合 计 (5)
10～ 20～ 30～ 40～ 50～ 60～ 70～ 80～ 90～ 100～ 110～ 120～ 130～ 140～ 150～ 160～ 170～ 180～ 190～ 200～ 210～ 220～ 230～ 240～ 250～ 260～	10 33 43 88 90 102 104 100 99 59 62 44 25 42 23 19 13 9 9 4 5 3 3 5 4 2	11.86 27.93 49.97 74.01 93.71 103.11 99.70 85.81 67.17 49.68 36.62 28.07 22.28 17.52 12.99(32.56) 8.80(19.57) 5.38(10.77) 2.94(5.39) 1.44(2.45) 0.64(1.01) 0.25(0.37) 0.12(0.12)	0.04 0.80 1.96 3.54 5.52 7.80 10.22 12.53 14.50 15.89 16.52 16.34 15.40 13.86 11.94 9.91 8.01 6.40 5.18 4.34 3.82 3.52 3.32 3.13 2.90 2.61	11.90 28.73 51.93 77.55 99.23 110.91 109.92 98.34 81.67 65.57 53.14 44.41 37.68 31.38 24.93 18.71 13.39 9.34 6.62 4.98 4.07 3.64 3.32 3.13 2.90 2.61
合 计	1000	800.00	200.00	1000.00

SGPT过高具有临床意义，按题意应取单侧95%上限(即第95百分位数，P₉₅)作正常值的界值。可从剖析得“正常人”样本，按百分位数法求P₉₅。为计算简便，可由大到小计算累计频数，见上表第(3)栏括号内数字，则
n₁(100-95)%=800(100-95)%=40,
故P₉₅在“140-”组段内。

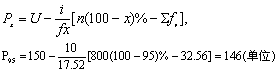
以SGPT 146（单位）划分正常与异常，其符合与错划概率，按式(5)～(8):

查标准正态分布表，φ(0.05)=0.5199,φ(0.05)=0.3984,

应用SGPT 146 （单位）作正常值上界，判别正常或有影响SGPT疾病的符合与错判概率，按式(9)～(12):

该医院取SGPT 146（单位）为单侧95%正常值上界，其假阳性率为5%，假阴性率为61.13%；在有、无影响SGPT疾病的人就诊比例不变的情况下，SGPT小于146（单位）者，有86.14%可能无影响SGPT的疾病，漏诊的可能性为13.86%。检验结果大于146（单位）者，有66.03%可能属肝功异常或有肌组织、脑组织等方面的损害（当然应结合其他医学检查来确诊），误诊的可能性为33.97%。