法向加速度
法向加速度faxiang jiasudu
运动质点的加速度在轨道法线方向上的分量。将质点在某一点的加速度矢量沿轨道切线和法线方向分解,则法向加速度反映质点运动速度在方向上的变化,其大小等于质点速率的平方除以轨道的曲率半径,即|aτ|=|v|3/ρ,式中|aτ|是质点在A点的法向加速度数值,|v|是质点在A点的速率,ρ是曲线在点A的曲率半径,ρ= 。法向加速度的方向指向曲线在点A的曲率中心O。若质点作圆周运动,其法向加速度的方向始终沿着圆半径指向圆心,所以又称向心加速度。凡是速度方向发生变化的质点都有法向加速度。质量为m的质点的法向加速度an的数值,取决于作用在质点上的合外力在轨道法线方向上的分量Fn(法向力)的大小,它们之间的关系遵循牛顿第二定律,即Fn=ma
。法向加速度的方向指向曲线在点A的曲率中心O。若质点作圆周运动,其法向加速度的方向始终沿着圆半径指向圆心,所以又称向心加速度。凡是速度方向发生变化的质点都有法向加速度。质量为m的质点的法向加速度an的数值,取决于作用在质点上的合外力在轨道法线方向上的分量Fn(法向力)的大小,它们之间的关系遵循牛顿第二定律,即Fn=ma 和an的方向沿曲率半径指向曲率中心的方向。因此,法向力Fn又叫向心力。
和an的方向沿曲率半径指向曲率中心的方向。因此,法向力Fn又叫向心力。
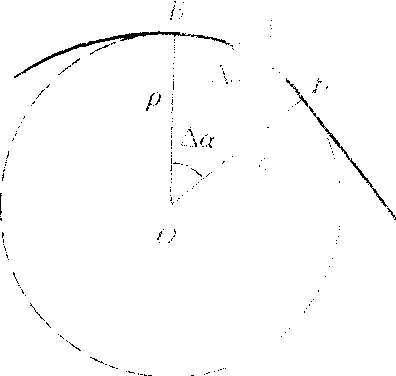
☚ 切向加速度 运动叠加原理 ☛
法向加速度
物体作曲线运动时所具有的沿轨道法线方向的加速度。其大小为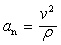 ,v为物体在该点的速率,ρ为曲线在该点的曲率半径。法向加速度只改变物体运动速度的方向。当物体作圆周运动时,其法向加速度就是“向心加速度”。参见“物理”中的“法向加速度”。
,v为物体在该点的速率,ρ为曲线在该点的曲率半径。法向加速度只改变物体运动速度的方向。当物体作圆周运动时,其法向加速度就是“向心加速度”。参见“物理”中的“法向加速度”。
法向加速度
质点作曲线运动时,所具有的沿轨道法线方向的加速度。数值上等于速度v的平方除曲率半径r,即v2/r。其作用只改变物体速度的方向,但不改变速度的大小。
- 莫辨楮叶是什么意思
- 莫达非尼是什么意思
- 莫迪亚诺是什么意思
- 莫迪克列亚尼是什么意思
- 莫迪利亚尼是什么意思
- 莫迪利亚尼,佛朗哥是什么意思
- 莫迪利亚尼,弗兰科是什么意思
- 莫迪利安尼,F·是什么意思
- 莫迪利安尼,F.是什么意思
- 莫迪利安尼-米勒定理是什么意思
- 莫迪博·凯塔是什么意思
- 莫迪塞恩是什么意思
- 莫迪格利安尼储蓄生命周期理论是什么意思
- 莫逆是什么意思
- 莫逆是什么意思
- 莫逆之交是什么意思
- 莫逆之交是什么意思
- 莫逆之交是什么意思
- 莫逆之交是什么意思
- 莫逆之交是什么意思
- 莫逆之交是什么意思
- 莫逆于心是什么意思
- 莫逊是什么意思
- 莫道不销魂,帘卷西风,人比黄花瘦是什么意思
- 莫道书生清苦意,比来食淡更精神是什么意思
- 莫道人行早,更有早行人是什么意思
- 莫道故人今白首,人虽有故心无旧是什么意思
- 莫道桑榆晚是什么意思
- 莫道桑榆晚,微霞尚满天是什么意思
- 莫道秋江离别难,舟船明日是长安。吴姬缓舞留君醉,随意清风白露寒是什么意思
- 莫邪是什么意思
- 莫邪是什么意思
- 莫邪三尺照人寒,试与挑灯仔细看。且挂空斋作琴伴,未须携去斩楼兰。是什么意思
- 莫邪为钝是什么意思
- 莫郁豪是什么意思
- 莫里是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克是什么意思
- 莫里亚克小说选是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹是什么意思
- 莫里兹短篇小说集是什么意思
- 莫里哀是什么意思
- 莫里哀是什么意思
- 莫里哀是什么意思
- 莫里哀是什么意思
- 莫里哀是什么意思
- 莫里哀是什么意思
- 莫里哀传是什么意思
- 莫里哀喜剧全集是什么意思