正常值范围估计

正常值范围的估计，就是根据正常人样本（或结合病人样本）数据，计算百分界值，以估计正常值范围。方法甚多，从实用的角度可分为两大类： 一类适用于正态分布或经变量变换能转换为正态分布的资料，最常用的是正态分布法，此外尚有对数正态分布法、正态概率纸法等；另一类适用于各种分布型资料，最常用的是百分位数法，此外尚有曲线拟合法、容许区间法等。
正态分布法 本法是根据正态分布规律，将正态曲线下的百分面积（相当于正常值范围的百分数）在横轴上的对应点作为正常值范围的界值。此法优点是结果较稳定，受两端尾部数据影响较小，也不受样本数据全距的限制；缺点是医学上很多资料不呈正态分布，不能用本法处理，即使一部分偏态分布资料可变换为正态分布，但手续较繁。本法步骤：
❶对资料作正态性检验(参见“正态性检验”);
❷当推断资料服从正态分布后，计算均数X与标准差s;
❸按式(1)估计正常值范围。

±uαs, (1)

式中u_α为正态曲线下面积为1-α时的标准正态（离）差，由表1查得。

表1 正常值范围估计常用uα值表

(1-α)百分数	单 侧	双 侧
80 90 95 99	0.842 1.282 1.645 2.326	1.282 1.645 1.960 2.576

例1 某地测得120例20～50岁正常人血浆结合¹²⁵碘-三甲状腺原氨酸(¹²⁵I-T₃)树脂摄取比值资料如下，求其双侧95%正常值范围。

125I-T3组段	0.75～	0.80～	0.85～	0.90～	0.95～
人 数	1	2	13	15	26
125I-T3组段	1.00～	1.05～	1.10～	1.15～	1.20～1.25
人 数	26	18	15	3	1

本资料经正态性检验服从正态分布，见条目“正态性检验”例2。并由该处表5第(1)～(5)栏得∑f=120,∑fx=-47,∑fx²＝381,i=0.05,X0=1.025，故

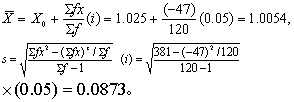
由表1查得双侧95%的u_0.05＝1.96，则

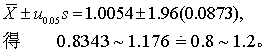
故该地20～50岁成人血浆结合¹²⁵I-T₃树脂摄取比值的双侧95%正常值范围可定为0.8～1.2。
对数正态分布法 医学上有一部分偏态分布资料可以通过对数变换转换为正态分布，然后按上法估计正常值范围。方法步骤如下：
(1)将观察值作对数变换。由于研究正常值范围的样本含量一般较多，结合频数表的编制(如表2)，用下法较为简便，即：
❶从观察值中找出最大值与最小值，并分别查出其对数。
❷参照对数全距划分对数组段（等距），并分别查出各组界的反对数，即成真数组段。其小数位数与观察值的小数位数相同，除后接尾数全为0外，末位一律进1。如例2，观察值均为整数，则真数组段的下限亦用整数。例2设计的对数组段见表2第(1)栏，因lg-10.45=2.82，则对数组段“0.45～”相应的真数组段用“3～”表示。但lg-11=10，则对数组段“1～”相应的真数组段用“10～”表示。
❸按真数组段划记频数。由此法编制的频数表尚可粗略估计是否为对数正态分布，若很不对称，即可否定其正态性。
(2) 正态性检验。
(3) 当推断资料服从对数正态分布后，计算对数值的均数X与标准差s。
(4)按式(1)估计正常值范围。(5) 最后把对数结果取反对数。
例2 1971年某市调查了200例正常成人血铅含量(μg/100g)如下，试估计该市成人血铅含量正常值的单侧95%上限。

17 17 17 17 17 18 19 19 19 20 20 20 21 21 21 22 22 22	18 18 18 18 19 19 19 20 20 20 20 20 21 21 22 22 22 23 23 23 24
24 24 24 24 24 25 27 28 28 29 29 30 32 32 32 32 33 33 43 47 50 53 60	25 26 26 26 26 26 27 30 31 31 31 31 32 32 36 38 38 39 40 41 41

(1)此资料属偏态分布，如表3第(1)、(2)栏，故试用对数变换，并编制频数表。
观察值的最大值为60,lg60=1.78；最小值为3,lg3=0.48。对数全距为1.78-0.48=1.30，设计组段并编制频数表见表2。(2)用矩法作正态性检验。
H₀: 总体服从对数正态分布，
H₁: 总体非对数正态分布。
α=0.05。
表2取缩简值见第(5)栏，则得n=200,∑fx=-100,∑fx²＝1504,∑fx2 =-2722,∑fx⁴＝ 28372。

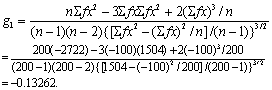
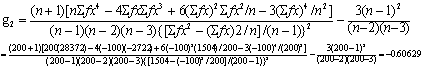
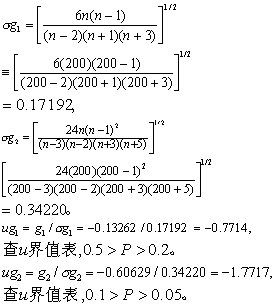
按α=0.05水准不拒绝H₀，可认为该市正常成人血铅含量服从对数正态分布。
(3)计算均数与标准差(均为对数值！)。

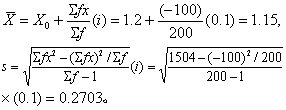
(4)估计正常值范围（对数值）。
查表1，单侧95%,u₀.₀₅＝1.645，则
+u0.0₅s=1.15+1.645×0.2703=1.5946。

表2 观察值对数变换及频数表的编制

对数组段 (1)	真数组段 (2)=lg-1(1)	划线记数 (3)	频数 (4)	x (5)
0.45～ 0.55～ 0.65～	3～ 4～ 5～	一 正 正正	1 5 10	-7 -6 -5
0.75～ 0.85～ 0.95～	6～ 8～ 9～	正正正正 正正一 正正正正一	20 11 21	-4 -3 -2
1.05～ 1.15～ 1.25～	12～ 15～ 18～	正正正正正 正正正正正 正正正正正正	29 25 30	-1 0 1
1.35～ 1.45～ 1.55～	23～ 29～ 36～	正正正正 正正正一 正	20 16 8	2 3 4
1.65～ 1.75～1.85	45～ 57～71	 一	3 1	5 6
			200

(5)取反对数，lg-11.5946=39(μg/100g)
故该市成人血铅含量正常值95%上限为39μg/100g。
正态概率纸法 本法用正态概率纸作图求解，最好在用正态概率纸作正态性检验的基础上进行，若散点基本在一直线上，则可认为资料服从正态分布。再通过图中各点，凭目测拟合一直线，尽量使点子交错地分布在直线上下，各点至直线平行于纵轴的距离力求短些，并重点照顾累计频率50%附近的点子。从纵轴上累计频率50%处作一水平线与直线相交，过交点作垂线与横轴相交，此处的横轴读数为均数；同理，纵轴上2.5%在横轴上的对应值，相当于“-1.96s”的位置，即双侧95%的下限；纵轴上97.5%在横轴上的对应值， 相当于“+1.96s”的位置，即双侧95%的上限；余类推。若用对数概率格纸，同样可在作对数正态性检验的基础上，由目测确定正常值范围，如例3。本法优点是简便快速，当样本含量较大，点子愈靠拢直线，准确性愈好。但由于拟合直线受分析者主观影响较大，不一定能得到最优直线，直线的斜率稍有不同，对上、下限的影响较大，而且读数亦有一定误差，故所得的结果仅是近似的估计值。
例3 对例2资料用对数概率纸作图求解。
对例2资料编制频数表，并求累计频率(%)，见表3。
将表3第(1)、(4)栏资料标在对数概率纸上，见下图，散点基本在一直线上，可认为此资料服从对数正态分布。用目测拟合一直线，直线上累计频率为95%时，读出横轴上的对应值约37μg/100g，即该市成人血铅含量正常值95%上限。与例2结果甚为相近。

表3 200例正常成人血铅含量的分布

血铅含量 (μg/100g) (1)	人 数 (2)	累计频数 (3)	累计频率(%) (4)
0～ 5～ 10～ 15～ 20～ 25～ 30～ 35～ 40～ 45～ 50～ 55～ 60～65	6 48 43 36 28 13 14 4 4 1 2 0 1	6 54 97 133 161 174 188 192 196 197 199 199 200	3.0 27.0 48.5 66.5 80.5 87.0 94.0 96.0 98.0 98.5 99.5 99.5 100.0

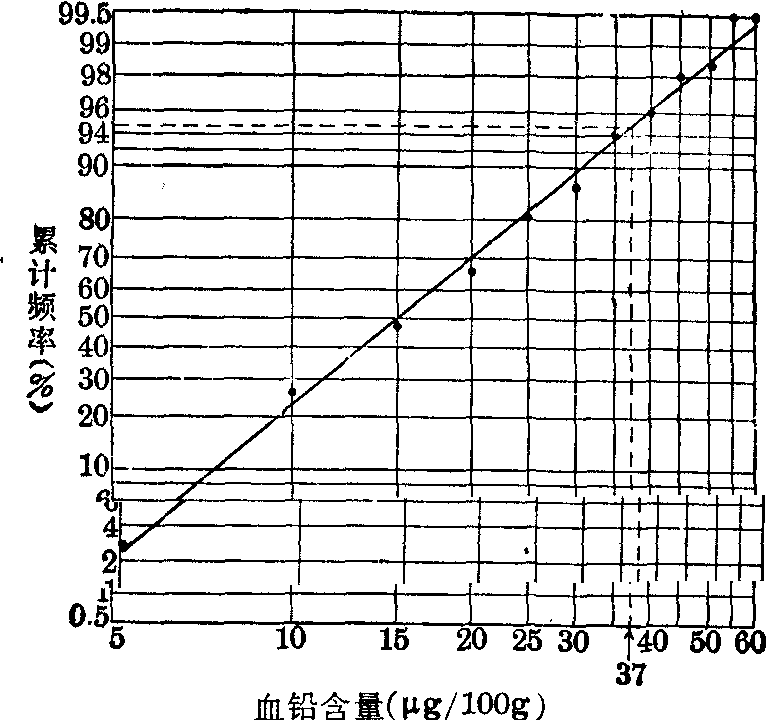
成人血铅含量正常值95%上限的估计

百分位数法 本法是用正常人样本的百分位数来估计正常值范围。百分位数的意义及其计算见条目 “百分位数”。应用本法的条件是样本含量较多，分布趋于稳定。其优点是可用于各种分布型资料（包括分布未知），简便快速，故颇为常用；缺点是受分布两端数据影响较大，而实际资料往往是愈近两端波动愈大。如表3资料，99%分位数(在“50～”组段) 不够稳定，而95%分位数 (在“35～”组段)就比较稳定了。它还受样本全距的限制，而样本含量较少时，往往全距较窄，因为抽到极端值的可能性较小。
例4 见条目“总体百分位数估计”例。
曲线拟合法 即对正常样本（或结合病人样本）的频数分布（包括经过变量变换），拟合某一理论分布或经验曲线，如拟合Poisson分布、二项分布、Gram-Charlier级数或其他曲线型；然后求出理论频数分布，再按百分位数法求解。或者由特制的工具表查出曲线下单侧或双侧百分面积在横轴上的对应界值，即所求的百分界值。或者用定积分按逐步逼近法求解，但较繁。本法一般计算均繁，当样本含量足够大时，与百分位数法结果很相近。容许区间法 容许区间常简写为TI。本法较为简便，其基本思想是： 将观察值由小到大排队，取Xr(秩次r所对应的观察值，下限)及Xg (秩次s所对应的观察值，上限)的区间作正常值范围，要求此区间内包括正常总体的一定百分数p，其把握度为γ。p与γ按设计要求选定。n（样本含量）、p与γ确定后，查特制的工具表及简单的计算即可求得r、s及Xr、 Xg。 类似的还有仅用于正态分布资料的K因子法， 即按±Ks(式中为均数、s为标准差)估计正常值范围，式中的K也是按指定的n、p与γ，查特制的工具表求得的。理论上当n=∞时，K值才等于表1的u值。