极大似然法
设f(x,θ1,θ2,…,θr)为随机变量ξ的密度函数,其中θ1,θ2,…,θr为未知参数,构造θ1,θ2,…,θr的似然函数L(θ1,θ2,…,θr),在使该似然函数极大的条件下估计未知参数θ1,θ2,…,θr的方法称为极大似然法。常被应用于测验分数统计中。
极大似然法
极大似然法
极大似然法是对总体参数θ作点估计的一个较好方法。 其优点是用它来求得的参数估计量 常能满足一致性和有效性等要求,并且具有不变性。 不变性指当
常能满足一致性和有效性等要求,并且具有不变性。 不变性指当 为θ的极大似然估计量时,则二者任何同一函数变换值,仍保持这种关系,比如lg
为θ的极大似然估计量时,则二者任何同一函数变换值,仍保持这种关系,比如lg  仍是lg θ的极大似然估计量。应用本法的前提是已知总体的分布,而未知其参数。对离散型分布,要已知概率函数p(X);对连续型要已知密度函数f(X)。本法是以从总体中抽得现有样本的可能性为最大的这一原则来确定参数的估计值。这里的可能性为最大也就是似然函数L(θ)为极大。
仍是lg θ的极大似然估计量。应用本法的前提是已知总体的分布,而未知其参数。对离散型分布,要已知概率函数p(X);对连续型要已知密度函数f(X)。本法是以从总体中抽得现有样本的可能性为最大的这一原则来确定参数的估计值。这里的可能性为最大也就是似然函数L(θ)为极大。
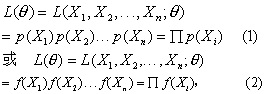
式中X1,X2,…,Xn是含量为n的样本。未知参数可以是一个,如θ;也可以是k个,如θ1,θ2,…,θk。
根据数学分析方法,当L(θ)的极大值存在时,将L(θ)对θ求一阶导数使之等于零,解得的能使L(θ)为极大的θ值,即
 ,这样求
,这样求 的方法称为极大似然法。
的方法称为极大似然法。例1 设一个含量为n的随机样本取自点二项分布的总体:
p(X)=πX(1-x)1-x,X=0、1,0≤π≤1。
求参数π的极大似然估计量。
按式(1),得似然函数及其自然对数为
L(π) =π∑Xi (1-π)n-∑Xi,ln L(π)=∑Xilnπ+(n-∑Xi) ln(1-π)。
求上式的导数,并使之等于零,
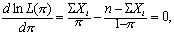
解之,得π的极大似然估计量为
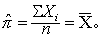
若总体的阳性率为π,当试验结果为阳性时,X=1;为阴性时,X=0。如果在n次试验中有k次为阳性,则∑Xi=k,于是
 =k/n=p。 即π的估计量为样本率p。例2 设X服从正态分布N(μ,σ2),求未知参数μ与σ2的极大似然估计量。
=k/n=p。 即π的估计量为样本率p。例2 设X服从正态分布N(μ,σ2),求未知参数μ与σ2的极大似然估计量。正态分布的密度函数为
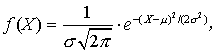
设X1 ,X2,…,Xn为所得样本的观察值,按式(2)得似然函数及其自然对数为
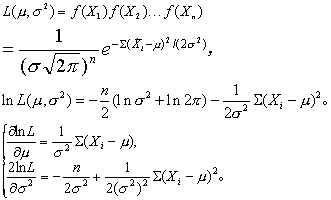
令此导数为零,并解之:
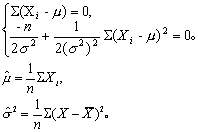
这便是μ与σ2的极大似然估计量。根据它的不变性,得
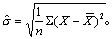
☚ 参数的点估计 可信区间 ☛
极大似然法
极大似然法maximum-likelihood method
求未知参数点估计的方法。劳利1940年提出。尤洛斯格等人1967年提出一个较为实用的计算方法后得到广泛使用。基本思想是,设已知一随机试验有若干不同结果A,B,C,…,如果在一次具体试验中A发生了,则可认为当时条件最利于A发生,故应选择使A发生概率最大的分布的参数。具体过程就是构造一个以观测值和未知参数为自变量的似然函数,并通过极大化此似然函数,从而获得模型的参数估计。
☚ 点估计 区间估计 ☛
- 前去的道路是什么意思
- 前去等候是什么意思
- 前去进行谴责并讨伐敌方的队伍是什么意思
- 前叉是什么意思
- 前发是什么意思
- 前发球线是什么意思
- 前发订单是什么意思
- 前发际是什么意思
- 前古未有是什么意思
- 前古未闻是什么意思
- 前古负材多为国,满怀经济欲何从。是什么意思
- 前只月是什么意思
- 前召后杜是什么意思
- 前可行性研究是什么意思
- 前台是什么意思
- 前司是什么意思
- 前吃后空是什么意思
- 前各工是什么意思
- 前合后仰是什么意思
- 前合后偃是什么意思
- 前合后堰是什么意思
- 前名恐惶是什么意思
- 前后是什么意思
- 前后一呼一应是什么意思
- 前后一致是什么意思
- 前后七国志是什么意思
- 前后七子是什么意思
- 前后三是什么意思
- 前后三光是什么意思
- 前后三段论是什么意思
- 前后不一样是什么意思
- 前后不通是什么意思
- 前后两矛是什么意思
- 前后两面同时攻击是什么意思
- 前后为难是什么意思
- 前后之屯是什么意思
- 前后互相接应是什么意思
- 前后交叉韧带断裂的关节镜诊断是什么意思
- 前后共同抵补是什么意思
- 前后关系是什么意思
- 前后出塞录是什么意思
- 前后劈叉双人座倒立造型是什么意思
- 前后劈腿是什么意思
- 前后受到敌人的夹攻是什么意思
- 前后叫应法是什么意思
- 前后因地是什么意思
- 前后园是什么意思
- 前后增大型双室肥大是什么意思
- 前后夹击,木华黎勇夺溜石山是什么意思
- 前后夹攻是什么意思
- 前后对比法是什么意思
- 前后展臂是什么意思
- 前后左右是什么意思
- 前后左右将军是什么意思
- 前后左右附近的地方是什么意思
- 前后座双人皮艇是什么意思
- 前后径是什么意思
- 前后徒言隔,相悲讵几晨。是什么意思
- 前后情况不同是什么意思
- 前后所有大街小巷是什么意思