曲线的切线和法线quxian de qiexian he faxian

若直线和曲线有两个相邻的交点P和Q，当Q点沿着曲线无限接近于P点，直线PQ的极限位置PT叫做这条曲线上经过P点的切线(如图1)，过P点垂直于切线的直线叫做曲线在P点的法线.

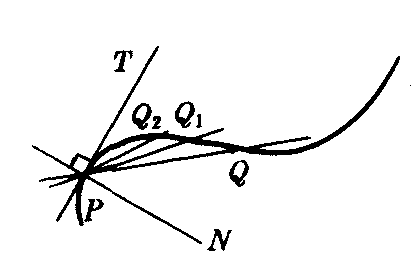
图1

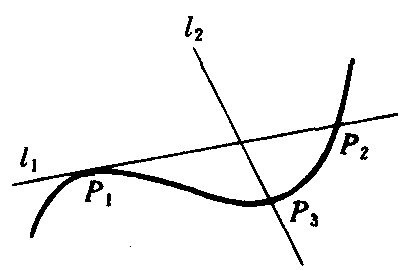
图2

平面几何中，和圆只有一个公共点的直线叫做圆的切线.这个定义，对于一般曲线的切线不适用，如图2，直线l₁和曲线有两个公共点，但它是曲线上经过P1点的切线；而直线l₂和曲线只有一个公共点，但它不是曲线的切线.
求经过曲线上一点P (x₁,y₁)的切线方程的一般方法是：
❶在曲线上取和P点邻近的一点Q(x₁+Δx,y₁+Δy)，把P,Q两点的坐标代入曲线方程，求出割线PQ的斜率Δy/Δx;
❷求出切线的斜率;
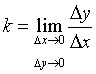❸把k代入方程y-y₁＝k(x-x₁)，并且利用P (x₁,y₁)适合于曲线方程的条件进行化简.
例 求曲线xy=a(a≠0)在P (x₁,y₁)点的切线方程(x₁≠0,y₁≠0).
解 设Q(x₁+Δx,y₁+Δy)是曲线xy=a上邻近P (x₁,y₁)的一点(Δx,Δy表示x₁,y₁的很小的改变量)；因为P,Q两点都在曲线上，所以

x1y1=a, (x1+△x)(y1+△y)=a

两式相减，得

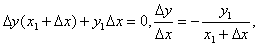
当Q趋近于P点， 即

△x→0,△y→0

时

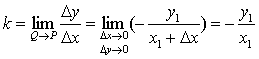
所求切线方程是

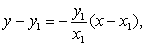
即

y1x+x1y=

2a.