普遍二次曲面的中心pubian erci qumian de zhonsxin

曲面上任意两点所联的线段叫做弦. 普遍二次曲面一组平行弦的中点的轨迹是一平面. 平分普遍二次曲面的一组平行弦的平面，叫做以该弦的方向为共轭方向的径平面. 普遍二次曲面的所有径平面形成一个平面族. 设普遍二次曲面的方程是F (x,y,z)≡ax²+by²+cz²+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0 (a²+b²+c²+f²+g²+h²≠ 0). 则三个平面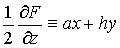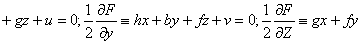+cz+w=0的交点叫做普遍二次曲面的中心. 当中心在曲面上 （即它是奇异点） 时，叫做顶点. 普遍二次曲面不是无轨迹的情况，且方程中一次项的系数都是零，则原点是它的对称中心； 反之，若原点是对称中心，则F (x,y,z) =0所有一次项的系数都是零. 普遍二次曲面不是无轨迹的情况，则中心就是它的对称中心，反过来，对称中心就是它的中心. 设上述三个平面方程构成的方程组的系数矩阵和增广矩阵分别是C及A，即

条 件	方程组解 的个数	中心的情况		曲 面 的 形 状
RC=3	唯一解	一个中心	非顶点	椭圆面 （实或虚）、 双曲面
			顶点	锥面 （实或虚）
RC=2 RA=2	含一个参 数的解	一条直线 的中心	非顶点	椭圆柱面 （实或虚）、 双曲柱面
			顶点	一对相交平面 （实或虚）
RC=1 RA=1	含二个参 数的解	一个平面 的中心	非顶点	一对相异或虚平行平面
			顶点	一对重合平面
RC=2 RA=3	无 解	没有中心	抛 物 面
RC=1 RA=2	无 解	没有中心	抛物柱面

它们的秩分别记作RC及R_A，则二次曲面中心的情况如下表：

条 件	方程组解 的个数	中心的情况		曲 面 的 形 状
RC=3	唯一解	一个中心	非顶点	椭圆面 （实或虚）、 双曲面
			顶点	锥面 （实或虚）
RC=2 RA=2	含一个参 数的解	一条直线 的中心	非顶点	椭圆柱面 （实或虚）、 双曲柱面
			顶点	一对相交平面 （实或虚）
RC=1 RA=1	含二个参 数的解	一个平面 的中心	非顶点	一对相异或虚平行平面
			顶点	一对重合平面
RC=2 RA=3	无 解	没有中心	抛物面
RC=1 RA=2	无 解	没有中心	抛物柱面