旋转法解作图题xuanzhuanfa jie zuotuti

利用旋转变换作图的方法.利用旋转变换，把某一线段或图形绕某一定点旋转到一个适当的位置后，使求作的元素和已知元素产生联系，这种作图的方法叫做旋转法.使用旋转法要注意选取旋转中心、旋转角及旋转方向.
例如，求作一个等边三角形，使它的三个顶点分别落在三条平行线上.
已知 l₁∥l₂∥l₃.
求作 等边△ABC，使A,B,C分别落在l₁,l₂,l₃上.

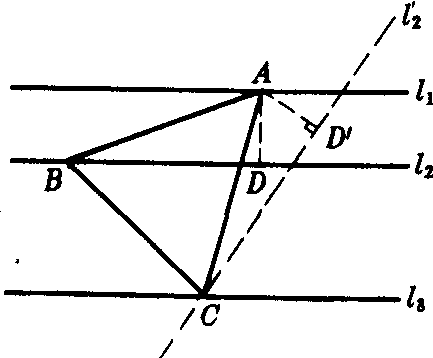
分析 如图，设△ABC是所求作的等边三角形.作AD⊥l₂于D.把△ABD绕点A旋转60°，则点B落在C点上，AD旋转到AD′的位置，l₂旋转到l₂′的位置.由于点B在l₂上，点C在l₃上，点B旋转后又与点C重合.所以点C应是l₂′和l_3′的交点.这样便可得到作图的方法.
作法
❶在l₁上任取一点A，作AD⊥l₂于D;
❷以AD为一边作∠DAD′=60°，且使AD^′=AD;
❸过D′作l₂′⊥AD′交l₃于C点；
❹连结AC;
❺作AB，使∠BAC=60°，交l₂于B;
❻连结BC.则△ABC就是所求的等边三角形.
证明 因为∠DAD′=∠BAC=60°，所以∠D′AC=∠DAB.又AD^′=AD,∠AD′C=∠ADB=90°，所以△AD′C≌△ADB，因此AC=AB.于是∠ABC=∠ACB，又因为∠ABC+∠ACB=180°-∠BAC=120°.所以∠ABC=∠ACB=60°.因此△ABC为等边三角形.
讨论 在这个问题中，假如每一相异的位置都作为一解，那么应有无数解.但是这个问题一般都认为是活位作图，所以只讨论形状大小，因此只有一解.