方差

在总体中指随机变量与其期望的差的期望，用σ²表示。在获得了总体的样本的观察值后，用各观察值与其算术平均值的偏差平方和的算术平均值来估计，记为s²_n，即s²_n＝(x_i-x-)²；在n不太大的场合，常用无偏估计s²＝(x_i-x-)²去估计σ²，其中n-1是偏差平方和(x_i-x-)²的自由度。若给出的是已经经过整理的频数分布表，用x₁,x₂，…，x_k表示可能的观察值（或组中值），用f_i表示观察到的x_i的个数，i=1,2，…，k，又记n=f₁+f₂+…+f_k＝f_ix-＝f_ix_i，则s²＝f_i(x_i-x-)²当x₁,x₂，…，x_k表示组中值时所求得的s²是一个近似值。常被应用于测验分数统计中。

方差variance

旧称变异量、变量。离均差的平方和与自由度的比值。常用σ2表示。由样本估计的方差又称均方，常用s2表示。表达式：

它是总体方差σ²的最好估计值。

式中n-1为自由度；N为有限总体所含个体数。

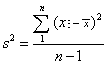
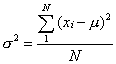
方差fangeha

设X是一个随机变量，若E [X-E (X)]²存在，则称它为X的方差，记作D (X)，即D(X) =E [X-E (X)]²，称为X的均方差或标准差。
由方差定义知，它是一个非负数，并且可知，若随机变量取值密集在数学期望附近，则方差小；反之则方差大。因此，D (X)是刻划X取值分散程度的一个数字特征。
方差具有以下性质：
❶D (C) =0,C是常数；

❷D (CX) =C²D (X);

❸设X,Y是相互独立随机变量，则

D(X +Y)==D(X)+D(Y),

D(X -Y)= D(X)+D(Y);

❹对于离散型随机变量，则有

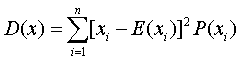
对于连续型随机变量，则有

方差也可以通过下述公式计算： D (X) =E (X)²-[E (X)]²。

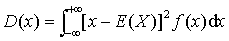
方差fang cha

又称变异数。用S²或V表示。是差异量数之一，代表一组数据的差异情况或离散程度。由各数据与平均数之差即离差自乘之和再除以数据个数而求得。公式为：

从公式可以看出，方差（变异数）是对一组数据中各种变异性的总和的测量，主要具有可加性特点。人们利用其可加性分解并确定出属于各种不同来源的变异性，如组间和组内，从而说明每一种变异性对总结果的相对影响，从而成为统计推论中常用的重要统计数。

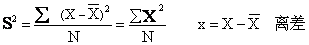
方差

表示随机变量ζ与其数学期望Eζ之间离散程度的一个量。即(ζ-Eζ)²的数学期望。通常记为Dζ或S²,Dζ=Eζ(ζ-Eζ)²。仿此可定义样本的方差S²＝1/n(x_i-)²，其中为样本x₁,x₂，…，x_n的平均数。这个量也反映了样本的离散程度。

方差variance

亦称变异数，是指总体中各变量值与其均数之差平方后的均数。用来表示变量值与其均数之间的离散程度。公式为：

实际应用中常以样本方差作为总体方差的估计值。样本方差的公式为：

式中σ²为总体方差，S²表示样本方差，X为变量值，μ为总体均数，X为样本均数，n为变量值的个数，∑表示总和。方差愈小，说明事物的离散程度愈小；方差愈大，说明离散程度愈大。

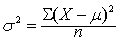
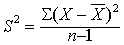
方差variance

指随机变量的所有可能值与其期望值之差的平方的期望值。通常用δ²表示。对于随机变量x，其方差为：
δ²＝E (x-Ex)²＝E (x-μ)²
式中，Ex=μ为X的期望值。对于变量的随机样本，其方差则等于样本观测值与样本均值之差的平方的均值， 通常用S2表示， s²＝1/N (x_i-x)²
其中，x₁为样本观测值，x为样本均值， x=1/Nx_i, N为样本容量。方差开算术平方根后所得之值δ,S分别为总体和样本的标准差。方差是衡量一个随机变量分布的离散程度的最重要的指标之一，一个随机变量的方差愈小，说明其分布愈集中，密集于它的数学期望值近。反之，方差越大，说明其分布愈分散。标准差也是衡量随机变量分布之离散程度的重要参数。

方差Variance

随机变量及其数学期望之间的偏离程度。计算公式为：V(x)=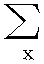(x-μ)²f(x)。其中，μ为随机变量的均值，f(x)为随机变量的概率密度函数。方差的性质：
❶变量的方差等于变量平方的平均数减变量平均数的平方；
❷变量对算术平均数的方差，小于对任何常数的方差；
❸n个同性质独立变量的方差等于各个变量方差之和；
❹n个同性质独立变量平均数的方差等于各变量方差平均数的1/n。

方差

衡量一个变量的样本观测值对其平均值的离散程度的指标。如一个变量X，其样本观测值为X_i,i=1,2,3，…，N。首先求得这些样本观测值的平均值，记为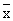；然后求出每个观测值与平均值的差，记为。这些差有的可能为正数，有的可能为负数。再对这些差进行平方，使其全部为正数，记为。最后求出其平均值，就是方差。以S²代表方差，其计算公式为：

对于一个随机变量来说，方差为其所有可能值与其期望值之差的平方的期望值。方差越小，表明其分布越集中于其期望值附近。方差的平方根，称为“标准差”。

方差

又称均方离差。是指总体中各标志值与其平均数的离差平方和平均数。其计算公式为：(1)对于未分组资料，

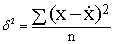
式中，δ²为方差，X为各个变量值，为各个变量值的算术平均数， n为变量值的个数。(2) 对于已分组资料，

式中，f为分配到各组的变量值的个数，Σf为各组变量值的频数之和。方差是测量变量离数度或标志变动度的最佳指标之一，计算出的方差数值越大，则变量值分布的离散度也越大，反之则越小。

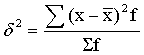
方差

标准差的平方。其性质：
❶变量的方差等于变量平方的平均数减变量平均数的平方；
❷变量对算术平均数的方差，小于对任意常数的方差；
❸n个同性质独立变量的方差等于各个变量方差之和；
❹n个同性质独立变量平均数的方差等于各变量方差平均数的1/n。

方差variance

标准差的平方。其性质：
❶变量的方差等于变量平方的平均数减变量平均数的平方；
❷变量对算术平均数的方差，小于对任意常数的方差；
❸n个同性质独立变量的方差等于各个变量方差之和；
❹n个同性质独立变量平均数的方差等于各变量方差平均数的1/n。

方差

在相同观测条件下，一组真误差平方的平均值之极限。

方差variance

差异量数的一种。随机变量ξ与其数学期望Eξ的偏差平方的加权平均E(ξ-Eξ)²。用Dξ或varξ表示。在概率论和数理统计中，表示随机变量和其数学期望（即均值）之间的偏离程度，即数据和中心偏离的程度。用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）。在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

方差

概率论的基本概念。随机变量ξ与其数学期望E ξ的偏差平方的加权平均E(ξ-E ξ)²。常记为Dξ或varξ。随机变量的方差由其概率分布唯一确定，故亦称某分布的方差。它表示随机变量取值的分散程度。方差愈大，该随机变量的取值愈分散。方差愈小，该随机变量取值愈集中。