抽屉原理Choutiyuanli

也叫鸽笼原理，是数学的基本原理之 一，基于以下事实：如果鸽子数多于笼子数，则至少有2只鸽子共一笼。根据鸽子数与笼子数，对于笼内的鸽子数作出判断。
抽屉原理I 把m+1件物品放入m个抽屉， 那么至少有一个抽屉中放了两件或两件以上这种物品。
例1:把10个乒乓球放入9个抽屉， 那么至少有1个抽屉中放了两个或更多的乒乓球。
例2:某年级有学生367人，证明至少有两人生日相同。
这是因为一年有365或366天， 因而有366种不同的生日，我们把这366种不同的生日看作“抽屉”，把367个人按各自生日归入相应“抽屉”， 这样根据抽屉原理， 至少有2人生日相同。
例3: 在100公里长的铁路线上建设11 个火车站， 那么至少有两个车站之间的距离不超过10公里。
我们把100公里长的铁路线每10公里一段分为10段，这10段作为“抽屉”， 火车站作为“物品”， 由抽屉原理，至少有两个火车站落在同一段内，它们之间的距离不超过10公里。
例4:任取5个自然数，证明，至少有两个数之差能被4整除。
证：把所有自然数分成4类，第一类是所有被4除余1的数，第二类是所有被4除余2的数，第三类是所有被4除余3的数，第四类是所有被4整除的数。这4类作为4个“抽屉”，任取的5个自然数作为5个“物品”， 由抽屉原理，至少有2个数取自同一类，它们被4除有相同的余数， 因此它们的差被4整除。
例4是把同余类作为“抽屉”，(参见《同余问题》，这类问题很常见，其一般形式为：任取k+1个自然数，其中至少有两个数的差能被k整除。
例5:某托儿所阿姨给5位小朋友分发糖果，每位小朋友至少分得一块， 证明必有一些小朋友分得的糖果数目之和能被5整除。
证：设5位小朋友分得的糖果数目分别为a₁、a₂、a3、a4、a5, 考虑下面的5个数， a1,a1+a2, a1+a2+a₃, a₁+a₂+a₃+a₄, a₁+a₂+a₃+a₄+a₅如果这5个数中某一个能被5整除，则问题已经解决，否则，这5个数分属5的4个同余类， (被5除余数分别为1、2、3或4), 由抽屉原理， 至少有两个数属于5的同一个同余类，它们的差被5整除，而这5个数中任意二个的差都是a1、a 2、a3、a4、a5中某些数的和， 问题得证。
使用抽屉原理解题，关键在于确定以什么作为“抽屉”，以什么作为“物品”，弄清抽屉与物品之间的数量关系， 有时，“抽屉”和“物品”的关系在题目中表现得比较隐蔽，需要仔细地观察分析，请看下面的例子。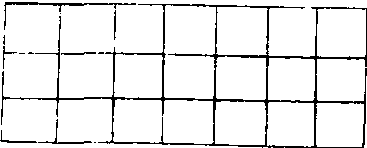
例6:如图，3×7=21个小方格， 每个小方格涂以红、黄、蓝三种颜色之一， 要求位于同一列的三个小方格所涂颜色两两不同，那么，至少有两列的涂色方式相同 （即从上到下有相同的颜色顺序）。
在这个问题中， 我们先考虑一列三个小方格的不同涂色方式， 自 上而下有1. 红、黄、蓝， 2. 黄、蓝、红.3. 蓝、红、黄. 4. 红、蓝、黄、5. 黄、红、蓝，6. 蓝、黄、红，共6种，把这6种不同的涂色方式作为“抽屉”，把7列作为7个“物品”， 由抽屉原理，可知至少有两列涂色方式相同。
例8:把50册书分赠给10名优秀学生，每人至少得一册，那么至少有2名学生得到的书册数相同。
如果10名学生得书册数两两不同，那么书的总数至少是1+2+3+…+10=55册， 而现在只有50册书，故至少有2人得书册数相同。此处按得书的册数不同划分“抽屉”，得书1册的，归入1号“抽屉”，得书2册的归入2号“抽屉”， 余类推。由于书的总册数小于55，可推知，实际使用的“抽屉”，数小于10，据抽屉原理即得结论。
抽屉原理Ⅱ 是抽屉原理的一般情形，把km+n(k、m、n是自然数)件物品放入m个抽屉，则至少有一个抽屉中有m+1件或者更多的物品。
例1: 假定年龄分别为21, 22, 23, …， 30岁的10个人围坐一圆桌，那么不论怎样安排坐次必有3个相邻的人年龄之和不小于77岁。
实际， 每相邻3人构成一相邻3人组，10人围坐一圈，就有10个相邻三人组，我们把一相邻3人组中3个人年龄之和称为该3人组的年龄，那么所有10个3人组年龄总和为
3× (21+22+23+…+30) =765。
把10个3人组看作10个“抽屉”，总年龄765岁看作“物品”，据抽屉原理Ⅱ，可知必有一个相邻3人组，该组中3人年龄之和不小于77。
例2:在纸上任取6个点，任意两点之间用红笔或者用兰笔连一条线(只准选一种颜色，连一条线)，那么在这六点中必可找到3点， 这3点两两之间的连线有相同的颜色。
固定6个点中的一个设为A, 考虑它与其它5点的5条连线的颜色，由于只有两种不同颜色，故至少有三条连线的颜色相同，不妨设为红色，假定这三条连线的异于A的端点分别为B、C、D，考虑B、C、D之间的连线颜色，若它们之间连线颜色相同，则问题解决，否则， 这三条连线中必有一条为红色， 其二端点与A之间的3条连线颜色相同。
抽屉原理与分类 抽屉原理可以用来进行一些存在性判断， 应用抽屉原理的关键在于正确地设置抽屉， 而设置 “抽屉” 与集合的分类常常是一回事。
例1: 随便找10个人， 其中至少有两人， 他们在10个人中相识的人数一样多。按认识的人数把10个人分成10类，一个人也不相识的算第一类， 只与1个人相识的算第二类， …， 与所有其他人相识的算第10类。由于人数与类数都是10，无法直接使用抽屉原理，但是若第1类不空， 就是说至少有1人与所有其他人不相识，那么第10类必为空，即没有人与所有人都相识，反之亦然，因此第一类与第10类至少有一类为空。这就是说10个人按上述方式分类， 至多有9类不空，把不空的类作为 “抽屉”， 应用抽屉原理即得结论。
例2: 某班40名学生算术考试得分总和为3 179分，又知每个人得分均在60分以上，那么至少有两个人成绩相同。按分数把全班学生分类，不同得分有41种可能 (从60到100), 因而分为41类， 无法直接应用抽屉原理。但若所有学生得分都不相同，那么总分至少是3 180分(60+61+…+99) 与题没矛盾， 因此，可能的41类中，至少有2类为空，即40名学生分为39或少于39类， 利用抽屉原理即得结论。
以上两例中，抽屉个数均不少于物品个数，不能直接使用抽屉原理， 但依题意可推知某一个或某几个抽屉是空的，而不空的抽屉数少于物品数。这时再利用抽屉原理得到结论。

抽屉原理

又称“鸽笼原理”、“狄里克雷原理”。其最简单的表达方式是：假如有n+1个（或更多个）物体装入n个抽屉中，那么一定有某个盒子至少装有两个物体。